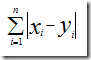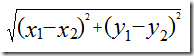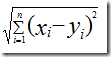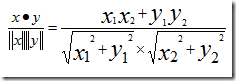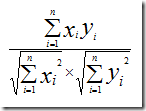推荐算法——距离算法
本文内容
- 用户评分表
- 曼哈顿(Manhattan)距离
- 欧式(Euclidean)距离
- 余弦相似度(cos simliarity)
推荐算法以及数据挖掘算法,计算“距离”是必须的~最近想搭一个推荐系统,看了一些资料和书《写给程序员的数据挖掘指南》,此书不错,推荐大家看看,讲解得很透彻,有理论有代码,还有相关网站。看完后,你立刻就能把推荐算法应用在你的项目中~
本文先主要说明如何计算物品或用户之间的“距离”,陆续会介绍推荐算法本身~
用户评分表
大体上,推荐算法可以有两种简单的思路:一是相似的用户,二是相似的物品。
前者,把与你相似的用户喜欢(或购买或评价高)的商品推荐给你,也就是说,如果你跟某个用户的喜好比较接近,那么就可以把这个用户喜欢的,而你不知道(或没浏览过,或没购买过等等)的物品推荐给你。什么叫“喜好接近”,就是对某些物品的评价也好,购买也罢,都比较接近,就认为,你和他喜好相同~
前者的缺陷在于,用户的评价毕竟是少数,想想,你评价过(显式评价)的物品有多少!大多数还是隐式评价,所谓隐式评价,如果你购买一个物品,那显然你会喜欢他,不然也不会买~因此,利用相似的用户是有局限性的。不如利用相似的物品来推荐。
下面“距离”算法主要针对计算用户之间的距离(相似性)。
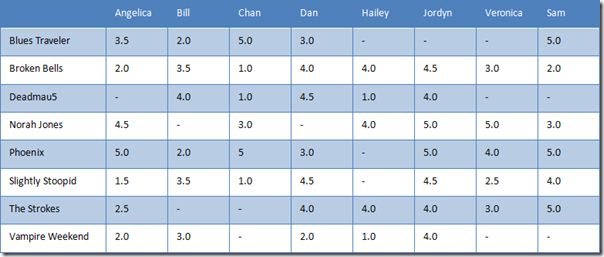
假设,8个用户对8个乐队进行评分,如下表所示。横向是用户,纵向是乐队。
表 1 用户评分表
曼哈顿(Manhattan)距离
计算距离最简单的方法是曼哈顿距离。假设,先考虑二维情况,只有两个乐队 x 和 y,用户A的评价为(x1,y1),用户B的评价为(x2,y2),那么,它们之间的曼哈顿距离为
因此,Angelica 与 Bill 之间的曼哈顿距离如下表所示。
表 2 Angelica 与 Bill 的曼哈顿距离
那么,Angelica 与 Bill 之间的曼哈顿距离为 9,即第二列减第三列的绝对值,最后累加。
注意,必须是这两个用户都评分的乐队。
可以推广到n个乐队,即n维向量,用户 A(x1,x2,…,xn),用户B(y1,y2,…,yn) ,那么它们之间的曼哈顿距离为
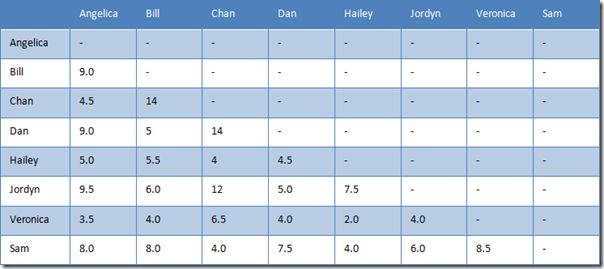
则用户之间的曼哈顿距离如下表所示。
表 3 用户之间的曼哈顿距离
曼哈顿距离的最大好处就是简单,只是加减法而已。如果有几百万个用户,计算起来会很快。
不仅可以扩展到 n 个乐队,当然也可以扩展到 m 个用户,它们可以形成一个矩阵。下面的其他距离同理。
Netflix 当初出 100 万美元奖励给能提升推荐算法 10% 准确率的团队或人,而赢得奖金的人就是使用了一种叫奇异矩阵分解的方法~
欧式(Euclidean)距离
除了曼哈顿距离外,还可以计算两个用户之间的欧式距离。
还是先考虑两个乐队 x 和 y 的情况,假设,用户A=(x1,y1),用户B=(x2,y2),那么它们之间的欧式距离:
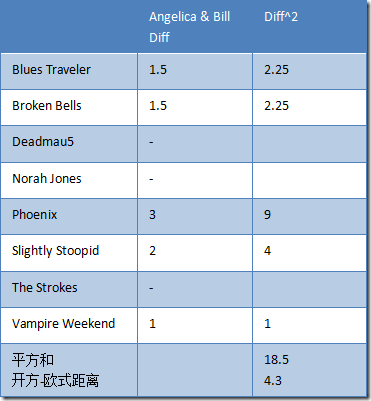
Angelica 与 Bill 之间的曼哈顿距离如下表所示。
表 4 Angelica 与 Bill 的欧式距离
推广到 n 个乐队,用户 A(x1,x2,…,xn),用户B(y1,y2,…,yn)
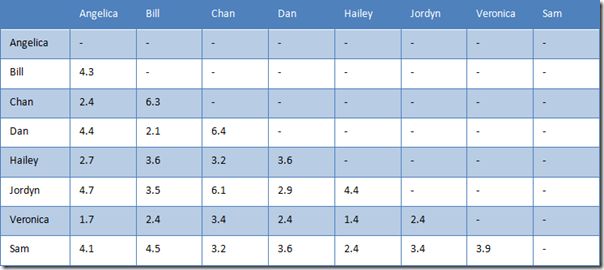
表 5 用户之间的欧式距离
但曼哈顿距离和欧式距离,有个缺点。对比一下 Hailey 与 Veronica 和 Jordyn,Hailey 与前者只有两个乐队评过分,而与后者是五个。换句话说,Hailey 与 Veronica 的距离是基于二维的,而 Hailey 与 Jordyn 是基于五维。想想都觉得有问题。
所以,曼哈顿距离和欧式距离适合数据比较稠密、缺失值比较少的情况。如果缺失值很多,余弦相似度就比较合适。
曼哈顿距离和欧式距离,有通用公式,称为闵可夫斯基距离(Minkowski Distance)。
余弦相似度(cos simliarity)
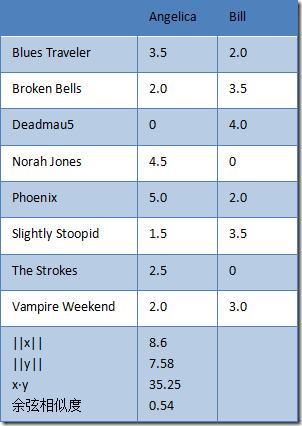
假设,有两个乐队,用户A=(x1,y1),用户B=(x2,y2),那么他们之间的余弦相识度为:
表 6 Angelica 与 Bill 的余弦相似度
推广到n维,用户A和B,对n个乐队的评分分别为(x1,x2,...,xn)和(y1,y2,...,yn),则他们之间的余弦相似度为
源代码 dis.py
#
# dis.py
#
from math import *
teams = [
"Blues Traveler",
"Broken Bells",
"Deadmau5",
"Norah Jones",
"Phoenix",
"Slightly Stoopid",
"The Strokes",
"Vampire Weekend"
]
users = {
"Angelica": {
"Blues Traveler": 3.5,
"Broken Bells": 2,
"Norah Jones": 4.5,
"Phoenix": 5,
"Slightly Stoopid": 1.5,
"The Strokes": 2.5,
"Vampire Weekend": 2
},
"Bill": {
"Blues Traveler": 2,
"Broken Bells": 3.5,
"Deadmau5": 4,
"Phoenix": 2,
"Slightly Stoopid": 3.5,
"Vampire Weekend": 3
},
"Chan": {
"Blues Traveler": 5,
"Broken Bells": 1,
"Deadmau5": 1,
"Norah Jones": 3,
"Phoenix": 5,
"Slightly Stoopid": 1
},
"Dan": {
"Blues Traveler": 3,
"Broken Bells": 4,
"Deadmau5": 4.5,
"Phoenix": 3,
"Slightly Stoopid": 4.5,
"The Strokes": 4,
"Vampire Weekend": 2
},
"Hailey": {
"Broken Bells": 4,
"Deadmau5": 1,
"Norah Jones": 4,
"The Strokes": 4,
"Vampire Weekend": 1
},
"Jordyn": {
"Broken Bells": 4.5,
"Deadmau5": 4,
"Norah Jones": 5,
"Phoenix": 5,
"Slightly Stoopid": 4.5,
"The Strokes": 4,
"Vampire Weekend": 4
},
"Sam": {
"Blues Traveler": 5,
"Broken Bells": 2,
"Norah Jones": 3,
"Phoenix": 5,
"Slightly Stoopid": 4,
"The Strokes": 5
},
"Veronica": {
"Blues Traveler": 3,
"Norah Jones": 5,
"Phoenix": 4,
"Slightly Stoopid": 2.5,
"The Strokes": 3
}
}
def manhattan(rating1, rating2):
"""Computes the Manhattan distance. Both rating1 and rating2 are dictionaries
of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
distance = 0
commonRatings = False
for key in rating1:
if key in rating2:
distance += abs(rating1[key] - rating2[key])
commonRatings = True
if commonRatings:
return distance
else:
return -1 #Indicates no ratings in common
def euclidean(rating1, rating2):
"""Computes the euclidean distance. Both rating1 and rating2 are dictionaries
of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
distance = 0
commonRatings = False
for key in rating1:
if key in rating2:
distance += pow(rating1[key] - rating2[key],2)
commonRatings = True
if commonRatings:
return sqrt(distance)
else:
return -1 #Indicates no ratings in common
def minkowski(rating1, rating2, r):
"""Computes the minkowski distance. Both rating1 and rating2 are dictionaries
of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
distance = 0
commonRatings = False
for key in rating1:
if key in rating2:
distance += pow(abs(rating1[key] - rating2[key]),r)
commonRatings = True
if commonRatings:
return pow(distance, 1.0/r)
else:
return -1 #Indicates no ratings in common
def cosineSimilarity (rating1, rating2):
"""Computes the Cosine Similarity distance. Both rating1 and rating2 are dictionaries
of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
sum_xy = 0
sum_sqr_x = 0
sum_sqr_y = 0
for key in teams:
if key in rating1 and key in rating2:
sum_xy += rating1[key]* rating2[key]
sum_sqr_x += pow(rating1[key], 2)
sum_sqr_y += pow(rating2[key], 2)
elif key not in rating1 and key in rating2:
sum_xy += 0
sum_sqr_x += 0
sum_sqr_y += pow(rating2[key], 2)
elif key in rating1 and key not in rating2:
sum_xy += 0
sum_sqr_x += pow(rating1[key], 2)
sum_sqr_y += 0
else:
sum_xy += 0
sum_sqr_x += 0
sum_sqr_y += 0
if sum_sqr_x ==0 or sum_sqr_y==0:
return -1 #Indicates no ratings in common
else:
return sum_xy / (sqrt(sum_sqr_x) * sqrt(sum_sqr_y))
def pearson(rating1, rating2):
"""Computes the pearson distance. Both rating1 and rating2 are dictionaries
of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
n = 0
for key in rating1:
if key in rating2:
n += 1
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += pow(x, 2)
sum_y2 += pow(y, 2)
# now compute denominator
denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
if denominator == 0:
return 0
else:
return (sum_xy - (sum_x * sum_y) / n) / denominator