假设检验——正态总体参数的检验（u检验，t检验，卡方检验，f检验）

【—–总体标准差已知时的单个正态总体均值的U检验——】

（1）分析：建立如下假设

（2）matlab进行检验：

% 调用ztest函数作总体均值的双侧检验，
% 返回变量h，检验的p值，均值的置信区间muci，检验统计量的观测值zval
[h,p,muci,zval] = ztest(x,100,2,0.05)   

结果：

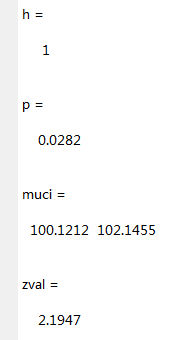
由h=1,p=0.0282<0.05拒绝原假设
且由置信区间的两个置信限都大于100，故作如下假设：
：=100

% 调用ztest函数作总体均值的单侧检验
[h,p,muci,zval] = ztest(x,100,2,0.05,'left') 

结果：

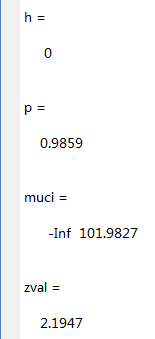
由h=0,p=0.9859>0.05接受上述接受即
所以该切割机不正常，总体均值大于100mm.

【—–总体标准差未知时的单个正态总体均值的t检验—–】

（1）分析：建立如下假设

（2）matlab进行检验：

x = [49.4  50.5  50.7  51.7  49.8  47.9  49.2  51.4  48.9];    % 定义样本观测值向量
% 调用ttest函数作总体均值的双侧检验，
% 返回变量h，检验的p值，均值的置信区间muci，结构体变量stats
[h,p,muci,stats] = ttest(x,50,0.05)

结果：

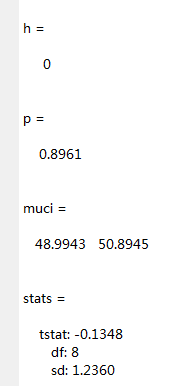
由h=0,p=0.8961>0.05知接受上述假设，即每包化肥的平均质量为50kg。

【——总体标准差未知时的两个正态总体均值的比较t检验—–】

（1）分析：建立如下假设

（2）matlab进行检验：

% 定义甲机床对应的样本观测值向量
x = [20.1,  20.0,  19.3,  20.6,  20.2,  19.9,  20.0,  19.9,  19.1,  19.9];
% 定义乙机床对应的样本观测值向量
y = [18.6,  19.1,  20.0,  20.0,  20.0,  19.7,  19.9,  19.6,  20.2];
alpha = 0.05;    % 显著性水平为0.05
tail = 'both';    % 尾部类型为双侧
vartype = 'equal';    % 方差类型为等方差
% 调用ttest2函数作两个正态总体均值的比较检验，
% 返回变量h，检验的p值，均值差的置信区间muci，结构体变量stats
[h,p,muci,stats] = ttest2(x,y,alpha,tail,vartype)

结果：

由h=0,p=0.3191知接受上述假设，即甲乙两台机床加工的产品的直径没有显著差异。

【——总体均值未知时的单个正态总体方差的卡方检验——】

例5.5：化肥厂用自动包装机包装化肥，某日测得9包化肥的质量（单位：kg）如下：
49.4 50.5 50.7 51.7 49.8 47.9 49.2 51.4 48.9
设每包化肥的质量服从正态分布，是否可以认为每包化肥的质量的方差等于1.5？取显著性水平
（1）分析：建立如下假设

（2）matlab进行检验：

% 定义样本观测值向量
x = [49.4  50.5  50.7  51.7  49.8  47.9  49.2  51.4  48.9];
var0 = 1.5;    % 原假设中的常数
alpha = 0.05;    % 显著性水平为0.05
tail = 'both';    % 尾部类型为双侧
% 调用vartest函数作单个正态总体方差的双侧检验，
% 返回变量h，检验的p值，方差的置信区间varci，结构体变量stats
[h,p,varci,stats] = vartest(x,var0,alpha,tail)

结果：

由h=0,p=0.8383知接受原假设，即每包化肥的质量的方差等于1.5。

【—总体均值未知时的两个正态总体方差的比较f检验—】

例5.6：甲乙两台机床加工同一种产品，从这两台机床加工的产品中随机抽取若干件，测得产品直径（单位：mm）为
甲机床：20.1, 20.0, 19.3, 20.6, 20.2, 19.9, 20.0, 19.9, 19.1, 19.9
乙机床：18.6, 19.1, 20.0, 20.0, 20.0, 19.7, 19.9, 19.6, 20.2
检验这两台机器机床加工的产品直径的方差是否相等？取显著性水平为0.05.
（1）分析：建立如下假设

（2）matlab进行检验：

% 定义甲机床对应的样本观测值向量
x = [20.1,  20.0,  19.3,  20.6,  20.2,  19.9,  20.0,  19.9,  19.1,  19.9];
% 定义乙机床对应的样本观测值向量
y = [18.6,  19.1,  20.0,  20.0,  20.0,  19.7,  19.9,  19.6,  20.2];
alpha = 0.05;    % 显著性水平为0.05
tail = 'both';    % 尾部类型为双侧
% 调用vartest2函数作两个正态总体方差的比较检验，
% 返回变量h，检验的p值，方差之比的置信区间varci，结构体变量stats
[h,p,varci,stats] = vartest2(x,y,alpha,tail)

结果：

由h=0,p=0.5798>0.05知接受原假设，即这两台机器机床加工的产品直径的方差相等。