NYOJ-1022合纵连横【并查集删除算法】

合纵连横

时间限制：1000 ms  | 内存限制：65535 KB

难度：3

描述

乱世天下，诸侯割据。每个诸侯王都有一片自己的领土。但是不是所有的诸侯王都是安分守己的，实力强大的诸侯国会设法吞并那些实力弱的，让自己的领土面积不断扩大。而实力弱的诸侯王为了不让自己的领土被吞并，他会联合一些其他同样弱小的诸侯国，组成联盟(联盟不止一个)，来共同抵抗那些强大的诸侯国。 强大的诸侯国为了瓦解这些联盟，派出了最优秀的间谍来离间他们，使一些诸侯国退出联盟。最开始，每个诸侯国是一个联盟。

有两种操作

1、U x y 表示x和y在同一个联盟。（0≤x，y<n）

2、D x   表示x退出联盟。

输入

多组测试数据
第一行两个数，n和m（1 ≤ n≤ 10^5, 1 ≤ m ≤10^5），分别表示诸侯国的个数和操作次数。
接下来有m行操作

输出

输出联盟的个数

样例输入

5 7

U 0 1

U 1 2

U 0 3

D 0

U 1 4

D 2

U 0 2

10 1

U 0 9

样例输出

Case #1: 2

Case #2: 9

 

这道题一读题，应该都能想到要用并查集归并集合。这道需要实现并查集的删除操作。那么问题就来了，并查集的的结构是一颗树，它的边是有向且只指向父节点的。那么删除一个节点（也就是让它的父节点成为它自己），指向这个节点孩子节点的根就会丢失。学习这个算法的时候网上说是用虚根，看了很久才看懂。

我就想用通俗更易懂的描述出来”虚根“：

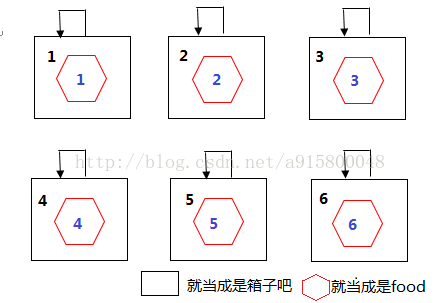
例子：食品店要给顾客甲派送食物food装在箱子box里，box有个挂钩（挂钩就相当于连接父节点的边）。food[]存储箱子编号，box[]存父节点。

food有很多，把要送的归在一类后。顾客甲打电话退订了某些。

如下图，food[2]=2.编为2的food它的箱子box编号是2

box[3]=3;编号为3的箱子box它的挂钩挂在自己上(它的父节点是它自己)。

 

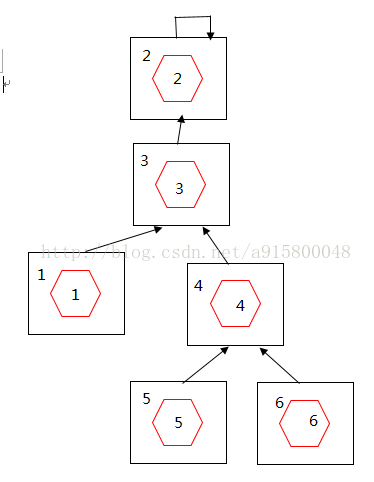
建立如下并查集树。box[3]=2;

 

然后顾客甲打电话要退订编号为4，6的food。

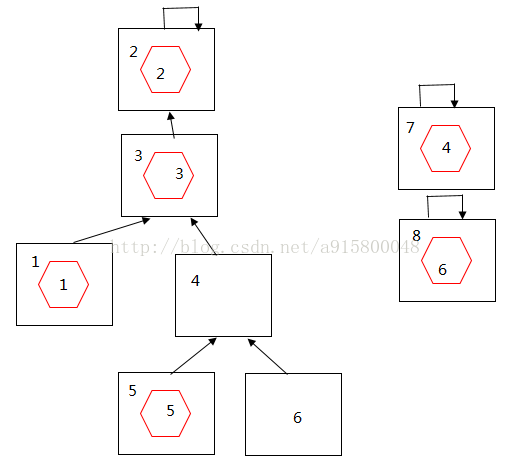
接下来我们只需要把编号为4的food拿走，用编号为n++（7）的箱子装起来。

food[4]=7;

box[7]=[7];

编号为4的箱子依然留在那里，这样就不影响编号4的box后面挂的箱子的根节点就不会丧失。

拿走6同理。

food[6]=8;

box[8]=8;

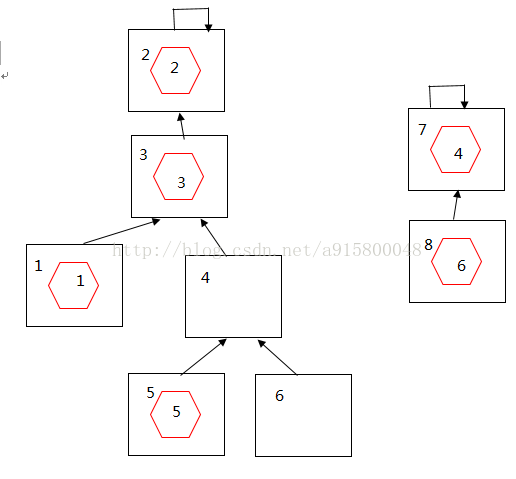
接下来又有一顾客乙要走了4,6.

box[food[6]]=food[4];\\把编号为6的food它所在的箱子8的挂钩挂到编号为4的food它所在的箱子7上。

food 2,3,1,5归顾客甲一类，food 4,6归顾客乙一类。这样虽然浪费了盒子但是归类是正确的。搜索x代表元,也就是通过x的箱子找到根箱子。

下附代码：

#include <stdio.h>
#include <string.h>
int box[1000050];
int food[1000050];
bool mark[1000050];
int find(int x)
{
	int f=x;
	while(box[f]!=f)
		f=box[f];
	int i=x;
	while(i!=f)
	{//路径压缩 也就是把根节点的孙直接作为根节点的儿子，减少了搜索次数
		int j=box[i];
		box[i]=f;
		i=j;
	}
	return f;
}
void Merge(int xx,int yy)
{
	int fx,fy;
	fx=find(xx);
	fy=find(yy);
	if(fx!=fy)
		box[fx]=fy;
}
int main()
{
	int n,m;
	char ch;
	int x,y;
	int ans;
	int count=1;
	int t;
	int i;
	while(~scanf("%d%d",&n,&m))
	{
		t=n;
		for(i=0;i<n;i++)
			{food[i]=i;box[i]=i;}
		for(i=0;i<m;i++)
		{
			getchar();
			scanf("%c",&ch);
			if(ch=='U')
			{
				scanf("%d%d",&x,&y);
				Merge(food[x],food[y]);//合并就是把箱子的挂钩钩上。
			}
			else 
			{
				scanf("%d",&x);
				food[x]=t;//删除：把food x拿出来装在t box 里。
				box[t]=t;//t box 挂钩钩自己
				t++;
			}
		}
		ans=0;
		memset(mark,0,sizeof(mark));
		for(i=0;i<n;i++)
		{
			if(mark[find(food[i])]==0)
			{mark[find(food[i])]=1;ans++;}				
		}
		printf("Case #%d: %d\n",count++,ans);
	}
	return 0;
}