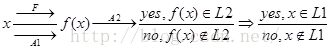算法导论之NP完全性和近似算法

NP完全性和近似算法

在理解NP完全性之前，笔者想引入关于科学与伪科学的定义。凡可接受实践检验、可被证实和被否正的为科学，相反之为非科学，而伪科学是非科学之子集，与科学相对立，认定非科学为科学的即是伪科学。三者关系可简化为：科学相反于非科学、对立于非科学子集伪科学。集合的运算关系见下面，科学定义为S、非科学定义为NS、伪科学定义为FS。

算法是用来解决问题的，一个问题能否在多项式时间内完成是衡量问题复杂度和算法有效性的标准。多项式时间就是指时间复杂度是个多项式。对于解决问题的算法，在其输入规模为下，其最坏运行时间为，其中k为常数，则问题在多项式时间内可解。显然，现实中很多问题是暂时无法找到多项式时间内的算法来解决，于是，以是否存在多项式时间内的算法来界定问题复杂度，存在则可解，反之则无解。NP集中在多项式复杂度的非确定性问题的研究上，属于科学，可被证实和被否正。

再说明下判定问题和最优化问题。判定问题是指寻求有穷步骤内确定是否具有某一特定的性质的一种能行方法或程序或算法，该类问题的答案可用“是否”来回答；最优化问题是在满足一定的约束条件和特定参数值输入下取得最佳值的可行解。对最优化问题的值设定一个界，可转化为相关判定问题。

特定状态输入下，如输出唯一确定，则为确定性算法，如输出多项可选，则为非确定性算法。非确定性算法将问题分解成猜测和验证两个阶段，算法的猜测阶段是非确定性的，算法的验证阶段是确定性的，它验证猜测阶段给出解的正确性。

P类问题（polynomialproblem）：多项式时间内可解的判定问题。

NP类问题（nondeterministic polynomial）：非确定性多项式时间可解的判定问题。

NPC类问题（NPcomplete）：属于NP中的问题，其复杂性与整个类的复杂性一致，其中一个存在多项式时间的算法，该类所有问题均可在多项式时间可解的。

通俗地说，P类问题就是多项时间内一定可解，可以很快解决的问题组成；NP类问题就是多项式时间内非确定性可解，在约束性的输入下，可以验证出多项式时间内的解，可以很快验证其解的问题组成；NPC类问题则是无法找寻一个多项式时间内的解的NP问题集合。显然，P和NPC都是NP的子集，且P和NPC无交集，如下面集合关系。

NPC问题的定性更多倾向于解决问题的难度或算法复杂度无法在多项式时间内量化，于是这类问题的集合在逻辑高度上便形成一即一切、一切即一的思维，一个问题有解，所有问题便有解。对于NP问题的非确定性算法，存在很多可能性的猜测，但结果正确与否可验证；可在多项式时间内验证一个解是否正确的问题即为NP问题，易验证问题类。

从NP类的问题中分出复杂性最高的一个子类，即NP完全类，其理论意义在于证明P=NP，只要二者有交集，就证明了NP类中的所有问题都是P类的，这对于解决NPC问题有现实意义。在算法设计和分析过程中,如证明某问题是NP完全的,即意味着面临hard问题；因此对于NP完全问题，寻找最佳近似算法，或者界定具体要求寻找多项式时间算法。

实际上，P、NP、NPC三者的集合关系随着各类难题的解决以及新出现的难题，证明P=NP一直未能有效成立。有解、未确定性有解、无解，就是问题的分类，有解的是P，如果能够证明无解的NPC有解，那未确定性有解的NP就是确定性有解。何谓未确定有解，无法证明有解，但如果提出一个解可以很快验证是否有效，其中找不到任何一个解的都归类到NPC，而NPC中只要有一个问题存在解，那所有该类问题都有解，这就是归约性的定义。

设A2是判定问题L2的多项式时间算法， F是计算规约函数f的多项式时间规约算法。

判定问题L1的多项式时间算法A1。x属于L1问题，将x通过F归约到f(x)，f(x)属于L2问题，如果f(x)能够通过多项式时间内的算法A2得解，则判定问题x可通过多项式时间算法A1得解。

反过来，归约性也用来证明一个问题在一个多项式时间因子内与其他问题一样难。通过归约性得出定理：如果任何NPC的问题是多项式时间内可求解的，则P=NP。等价地，如果NP中的任何问题不是多项式时间可求解的，则所有NPC问题都不是多项式内可求解的。目前理论研究的进展，倾向P不等于NP，三者的集合关系如下图。

既然NPC问题的存在，使P=NP不成立，那么研究NPC问题的解决便成为复杂类问题的关键。一般解决策略有：只对问题的特殊实例求解、用动态规划法或分支限界法求解、用概率算法求解、只求近似解、用启发式方法求解。关于近似算法定义如下：

如果对规模为n的任何输入，由近似算法产生的解的代价C与最优解的代价C*只差一个因子ρ(n)（近似比，approximation ratio），则该算法为ρ(n)近似算法。

若对问题的输入规模n，有一函数ε(n)使得，则称ε(n)为该近似算法的相对误差界。近似算法的性能比ρ(n)与相对误差界ε(n)之间显然有如下关系：。

对理解NPC和近似算法还需要就具体问题的算法求解进行研究，如旅行商问题、集合覆盖问题等。考验逻辑的图灵停机问题却想理解下。

图灵停机问题的描述：不存在一个程序（或算法），它能够计算任何程序在给定输入上是否会结束（停机）。用反证法来证明：

1）假设存在万能程序God_algo，可以判定任何一段程序及其给定的输入是否会结束。

boolGod_algo(char* program, char* input){

    if(<program> halts on <input>)

        return true;

    return false;

}

显然这个程序可以知道任何程序能否结束的结果，如果可以结束就返回true，不能结束就返回false。

2）现在我们增加一个程序Satan_algo来调用万能程序God_algo：

boolSatan_algo(char* program){

if(God_algo(program, input) ) {

       while(1);        // loop forever!

       return false;   // can never get here!

}else returntrue;

}

该程序根据God_algo返回结果输出。假设输入程序A，God_algo判定A程序及其给定输入input可停机，则进入循环无法退出，如果不停机则返回true。

3）Satan_algo调用自身：

Satan_algo（Satan_algo）执行结果显然是左右矛盾。

假设Satan_algo能够停机，God_algo返回ture，进入while循环，无法停机；

假设Satan_algo不能停机，God_algo返回false，返回true，可以停机。

4）结论：

Satan_algo能够停机=>Satan_algo(Satan_algo)它不能停机

Satan_algo不能停机=>Satan_algo(Satan_algo)它能够停机

推导出不存在这样的一个万能程序，可判定任何程序在给定输入下是否能停机。

科学的伟大就在于不断证明和反证明，科学家的伟大在于在不断的探索中肯定和否定，而思考和逻辑显然在这中间扮演着无穷魅力的角色。没有思考不存在逻辑，而没有逻辑的思考不存在思考的意义，沉浸在理论科学的汪洋大海中，忘记技术工程的琐细，是一种享受，而寻找理论的应用却是一种自我升华和证明的过程。现代信息科学大厦的基础无疑是数学，但计算机科学也丰富了数学的理论，无法忘记归纳、推理在程序中所体现的闪光点，图灵机开创的时代，至今令人心惊动摇，如今智能和量子时代的来临，图灵理论基础还是适用。要继续进步，也许只有理论再次创新，出现二次图灵机理论，每次理论的创新都有着漫长理论应用的经验探索，而后量变出现质变，我相信这个理论革命不远了。超越图灵机、突破冯诺依曼体系，是赋予现如今计算机科学理论研究者的使命，而作为前沿技术工程者，无疑是期待着能参与，可惜理论所需要的数学基础非专攻不能。