HDU 1542 Atlantis
【题目链接】点击打开链接
【题意】求矩形面积交,扫描线经典题!
【分析】浮点数先要离散化;然后把矩形分成两条边,上边和下边,对横轴建树,然后从下到上扫描上去,用mark【mark的作用到今天才搞明白,为什么要记录下底边和上底边差的个数,作用是为了统计总的下底边的长度sum时不出错,使得不会重复计算某个面积】表示该区间下边比上边多几个。线段树操作:update:区间增减 query:直接取根节点的值!
【补充】其实这样扫描相当于把给定的矩形通过边又分成若干个举行进行计算,而统计总下底边进行计算相当于同时计算多个矩形的面积,达到效率增快!
【扫描的过程】
struct tree{
double l,r,h;
int d;
tree(){}
tree(double x1,double x2,double y,int c):l(x1),r(x2),h(y),d(c){}
bool operator <(const tree &a)const{
return h<a.h;
}
}s[MAX];
s表示一条线段,分别有线段的左右端点l,r,线段的高h,线段是矩形的上底边还是还是下底边d:-1/1,
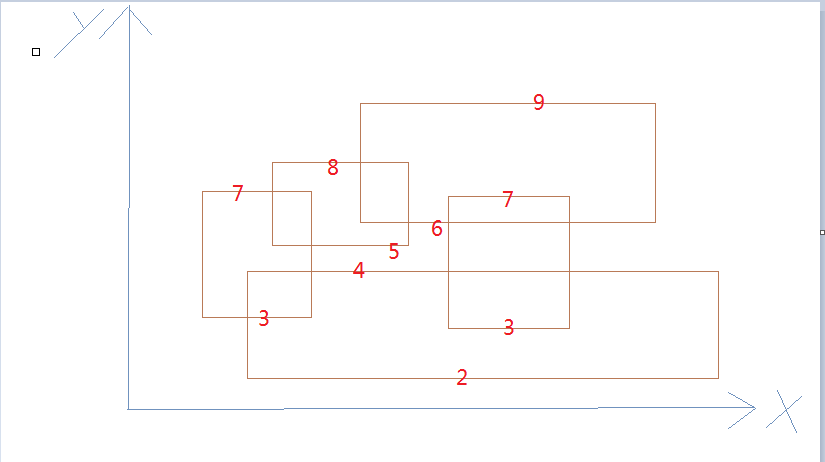
假设给出的矩形如上图,红色字表示相应边的高,
共9条线段
经从小到大排序后的边的高度h是:2,3,3,4,5,6,7,7,8,9
相应的d是:1,1,1,-1,1,1,-1,-1,-1,-1
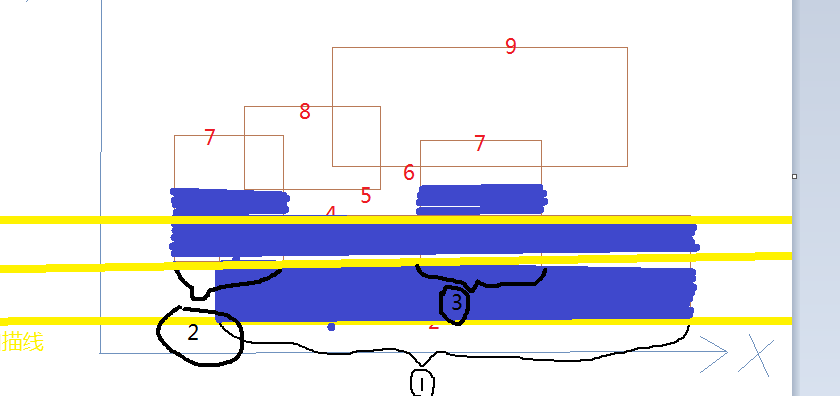
1,对第一条线段进行扫描:
得到的总下底边长sum[1]为黑色线部分,同时mark标记某个区间的下底边情况,1表示该区间(线段)全部可作为下底边
的到的面积ans+=sum[1]*(s[i+1].h-s[i].h)即为蓝色部分
2,对第2条线段继续扫描
sum为1.,2两部分合起来的总长度,此时s[3].h-s[2].h
=3-3=0,所以增加的面积是0
对第3条线段继续扫描
得到的总底边长度不变,新增加的面积为新增加的蓝色区域,忘记说了经过扫描后,得到2线段和3线段之间的mark=1,因为该区域下底边比上底边多就只有一条,1线段和2,3线段交集部分mark,因为上下底边差为2条
对第4条线段扫面,即高为4的那条线段,由于这条线段为上底边,所以d=-1,所以扫描后2线段和3线段之间的mark为0(1+-(1)=0),其余部分为1,则重新得到的总下底边sum[1]为线段2和线段3的长度
新增加的面积为蓝色面积
后面同理继续扫面线段增加新面积...........
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int maxn = 2202;
int mark[maxn<<2]; //记录某个区间下底边的个数
double sum[maxn<<2]; //记录某个区间下底边的总长度
double Hash[maxn]; //对x进行离散化,否则x为浮点数且很大无法线段树
//以横坐标作为线段(区间),对纵坐标线段进行扫描
//扫描的作用是每次更新下底边总长度和下底边个数,增加新面积
struct seg{
double l,r,h;
int d;
seg(){}
seg(double l,double r,double h,int d):l(l),r(r),h(h),d(d){}
bool operator<(const seg &rhs) const{
return h<rhs.h;
}
}s[maxn];
void Push_Up(int l,int r,int rt){
if(mark[rt]) sum[rt] = Hash[r+1] - Hash[l];//表示该区间整个可作为下底边
else if(l==r) sum[rt] = 0;
else
sum[rt] = sum[rt<<1]+sum[rt<<1|1];
}
void Update(int L,int R,int d,int l,int r,int rt){
if(L<=l&&r<=R){//该区间是当前扫描线段的一部分,则该区间下底边总长以及上下底边个数差更新
mark[rt] += d;//更新下底边相差个数
Push_Up(l,r,rt);
return ;
}
int m = (l+r)>>1;
if(L<=m) Update(L,R,d,l,m,rt<<1);
if(m<R) Update(L,R,d,m+1,r,rt<<1|1);
Push_Up(l,r,rt);
}
int binarysearch(double key,double *x,int n){
int l=0,r=n-1;
while(l<=r){
int m = (l+r)>>1;
if(x[m]==key) return m;
if(x[m]>key) r = m-1;
else l = m+1;
}
return -1;
}
int main(){
int n,num=0;
double x1,x2,y1,y2;
while(~scanf("%d",&n)&&n){
int k=0;
for(int i=0; i<n; i++){
cin>>x1>>y1>>x2>>y2;
Hash[k] = x1;
s[k++] = seg(x1,x2,y1,1);
Hash[k] = x2;
s[k++] = seg(x1,x2,y2,-1);
}
sort(Hash,Hash+k);
sort(s,s+k);
int m = 1;
for(int i=1; i<k; i++)//去重复端点
if(Hash[i]!=Hash[i-1]) Hash[m++] = Hash[i];
double ans=0.00;
memset(mark,0,sizeof(mark));
memset(sum,0,sizeof(sum));
for(int i=0; i<k; i++){//扫描线段
int L = binarysearch(s[i].l,Hash,m);
int R = binarysearch(s[i].r,Hash,m)-1;
if(L<=R) Update(L,R,s[i].d,0,m-1,1); //扫描线段时更新底边长度和底边相差个数
ans += sum[1]*(s[i+1].h-s[i].h);//新增加面积
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",++num,ans);
}
return 0;
}