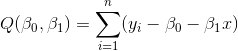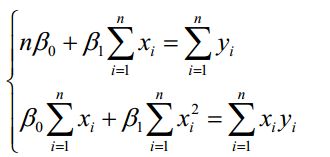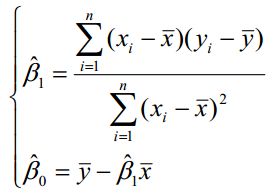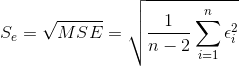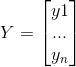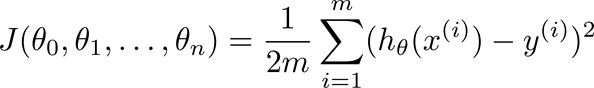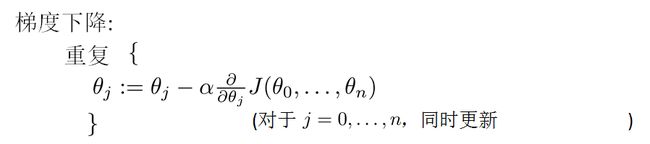SparkML之预测(一)线性回归分析理论部分

-------------------------------------------------------一元线性回归----------------------------------------------------------------------------

模型

反应一个因变量与一个自变量之间的线性关系，一元线性回归模型如下：

                                                         （1）

其中：

、：回归系数

：自变量

：因变量

：随机误差，一般假设服从

那么可以得到结论就是：服从

若我们之前对 (,)进行了 n次观测，那么就可以得到如下，一系列的数据

  为(1,2,...n)

那么把這些数值，带入(1)公式，那么就有 n个包含、方程，大家知道当要确定n个参数的时候，满秩的情况下，只要n个方程就就可以确定了，那么如何根据历史的观测数据来选择，来选择最佳的、，只要把、确定了，那么我们随便输入一个，就可以得到一个，那么选择一个"未来"的,就可以计算一个"未来"的,那么就达到了预测效果

普通最小二乘法

那么什么才是最佳的 、，最小二乘法的思想就是把决定后的方程，代入参数使得方差最小，就是最佳的。我们把全部的方差记为:

                               

那么现在就是计算关于参数、的极小值，当关于参数、的偏导为0的时候，那么取到极值

           

对其进行整理，得到如下：

              

那么可以直接计算出：

当自变量x多的时候，就很难直接计算、、....、，那么就必须用克拉姆法则（Cramer's Rule）计算，

其中，、、、是、、....、的最小二乘估计。

拟合效果分析

1、残差的样本方差

残差: （i = 1，2，...n）

残差的样本均值：

那么残差的样本方差:

其中n-2是自由度，因为有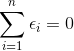和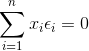约束，所以自由度减2（残差之间相互独立，残差和自变量x相互独立），如果我们的拟合方程：解释因变量越强，那么MSE是越小。你会发现：

这个MSE就是总体回归模型中方差的无偏估计量。

那么它的标准差：

2、判定系数（R）

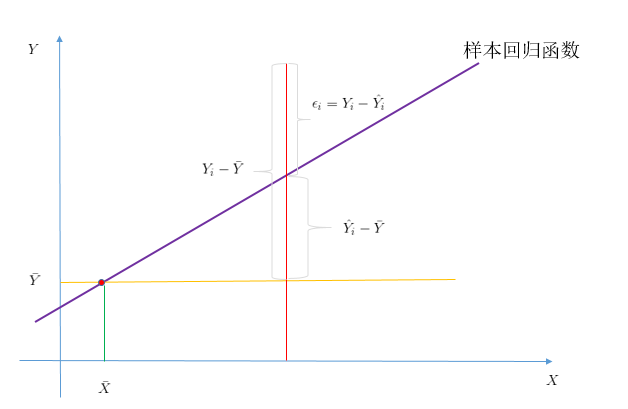
我们从新考虑我们的样本回归函数：

因为我们的解释变量的平均值,一定会经过我们的样本回归函数，下面证明：

两边进行平方之后再加总，然后除以样本容量n：

其中，，得到：

下面结合图像进行说明：

结合图像，我们可以得到下面方程：

两边平方之后，进行加总，得到：

:样本观测值和其平均值的离差平方和，自由度为n-1

:拟合直线可解释部分的平方和，自由度为1

:样本的观测值和估计值之差的平方，既残差平方和，自由度为n-2

缩写全拼（采用国外教材的缩写方式）：

Total sum of squares（SST）：总离差平方和

Residual sum of squares (SSR)：残差平方和

explained sum of squares(SSE):回归平方和（国人根据实际意义自己命名的？）

所以我们有：

那么对于我们真正解释了的部分和总体的比值（用表示）：

当时，也就是SSR = SSE,那么就是说原始数据完全可以拟合值来解释，此时SSR = 0，那么拟合非常完美

一般。

SSR很好计算，就是样本的实际观察值与估计值差的平方，所以用SSR去计算R

显著性检验

当你拟合好参数的时候，你要去评定一个這样的一个模型对于我们想要解释的问题是否显著(只有R是不够的)，

如果不显著那么就需要换其他模型方法了。对于其中检验的方法有F检验和T检验，本文重点是SparkMlib下的线性回归，本节只是一个铺垫，所以具体如何检验，就不赘述了。

-------------------------------------------------------多元线性回归----------------------------------------------------------------------------

模型

反应多个因变量与一个自变量之间的线性关系，多元线性回归模型如下：

（2）

其中：，都是与无关的未知参数，是回归系数。

现在得到n个样本数据（）,=1,....,n,其中,那么（2）得到：

（3）

我们可以把（3）写成如下模式：

（4）

其中：

,,,

求解过程和一元线性回归一样，可以得到:

判定系数（R）还是按照一元回归那样求解，当R大于0.8才认为线性关系明显

===================================最小二乘法的缺陷============================

1、只有当X满秩的时候，才可以用最小二乘法。因为在求解的时候的条件：X是满秩的，也就是在决定多个因变量

必须是相互独立的，当如果和有关联，可以用表示，那么X就不是满秩的

此时用最小二乘法就是错误的，因为X是不可逆的

2、最小二乘的复杂度高，在处理大规模数据的时候，耗时长。

--------------------------------------------------------------------梯度下降法-------------------------------------------------------------------

由于最小二乘法在求解时，存在局限，所以在计算机领域一般采用梯度下降法，来近似求解

为了与文献2的符号一致，所以放弃前面用过的符号，采用文献2中的符号。现在直接从多元线性回归开始

线性方程：

我们让,那么方程变为：

若我们之前对 (,)进行了 m次观测，那么就可以得到如下，一系列的数据

  为(1,2,...m),按照前面的思路，我们来计算“相差”多少,既所说的cost function：

（小插曲：不知道为什么有很多人把上面的m给省略了，在andrew NG课程中和Spark源码理解中都有这个m

其实加上m更能体现问题）

也就说让最小。如果用之前的最小二乘法，那么就是，让对求偏导，让等式都等于0，建立方程，联合求解：

我们知道最小二乘法的弊端，所以采用梯度下降法来求解最优的:

其中是学习效率，而且迭代的初始值设置为n+1列的零向量，然后一直迭代，直到收敛为止。

当样本很大的时候，如果迭代次数很大，那么我们会选择一部分样本进行对的更新计算。

更多细节，请看：http://write.blog.csdn.net/postedit/51277141

----------------------------------------------------------------------------------------------------------------------------------------------------

SparkML实验：

package Regression

import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint, LinearRegressionModel, LinearRegressionWithSGD}
import org.apache.spark.{SparkConf, SparkContext}

/**  * Created by legotime on 2016/4/17.  */ object RegressionWithSGD {
  def main(args: Array[String]) {
   val conf = new SparkConf().setAppName("LinearRegressionWithSGDExample").setMaster("local")
    val sc = new SparkContext(conf)

    // Load and parse the data
    val data = sc.textFile("E:\\SparkCore2\\data\\mllib\\ridge-data\\lpsa.data")
    val parsedData = data.map { line =>
      val parts = line.split(',')
      LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
    }
    /**parsedData形式：  * (-0.4307829,[-1.63735562648104,-2.00621178480549,-1.86242597251066,-1.02470580167082,-0.522940888712441,  * -0.863171185425945,-1.04215728919298,-0.864466507337306])  */   // Building the model
    val numIterations = 100//迭代次数
    val stepSize = 0.00000001//步长
    val model = LinearRegressionWithSGD.train(parsedData, numIterations, stepSize)//训练模型

    // Evaluate model on training examples and compute training error
    val valuesAndPreds = parsedData.map { point =>
      val prediction = model.predict(point.features)
      (point.label, prediction)
    }
    val numCount = valuesAndPreds.count()
    println("The sample count"+numCount)

    val MSE = valuesAndPreds.map{ case(v, p) => math.pow((v - p), 2) }.mean()//残差的样本方差
    println("training Mean Squared Error = " + MSE)
    println("模型的权重"+model.weights)
    println("模型的残差"+model.intercept)

    // Save and load model
    model.save(sc, "E:\\SparkCore2\\data\\mllib\\ridge-data\\scalaLinearRegressionWithSGDModel")
    val sameModel = LinearRegressionModel.load(sc, "E:\\SparkCore2\\data\\mllib\\ridge-data\\scalaLinearRegressionWithSGDModel")

    sc.stop()

    /**  * The sample count：67  * training Mean Squared Error = 7.4510328101026  *模型的权重[1.440209460949548E-8,1.0686674736254139E-8,9.608973495307957E-9,4.553409983798095E-9,1.2221496560765207E-8,8.910773406981891E-9,5.5962085583952E-9,1.2255699128757168E-8]  *模型的残差0.0  */   }
}

参考文献：

1andrew NG线性回归课件：链接：http://pan.baidu.com/s/1bTgHgq 密码：7mbt