二叉搜索树(搜索二叉树)转换成一个双向链表
1.题目描述:
将一个二叉搜索树转换成一个双向链表;
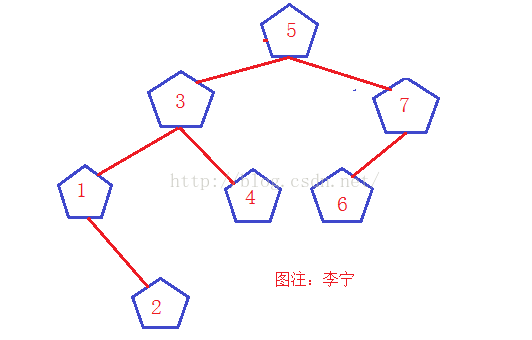
2.二叉搜索树,直接看图:
如图就是一个二叉搜索树的模型,也就是转换函数的入口数据,也是下边函数中即将用到的例子,既然有输入,肯定有输出,先面在看一张图(第三条):
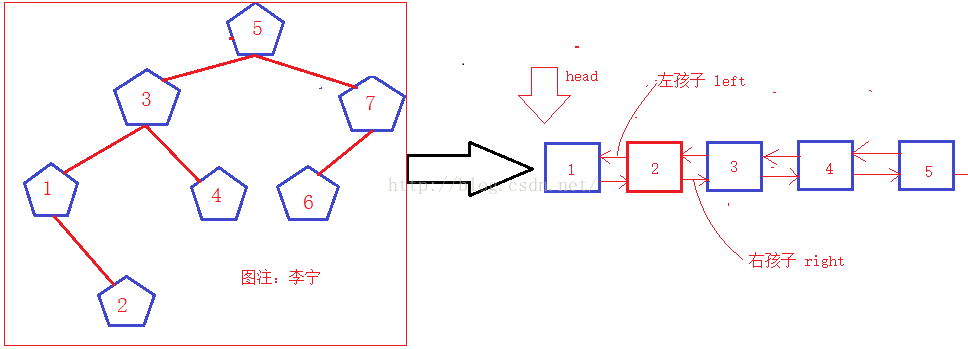
3.输入输出模型:
右边就是最终的输出结果,5后边是空,下边来分析一下:
1.在二叉搜索树中,每个节点都有两个孩子,即左和右,而在双向链表中,每个节点也有两个指针,前驱和后继指针,二叉树和双向链表很有相似性;
2.改变二叉搜索树的左右孩子指针指向,就可完成二叉搜索树到双向链表的转换;
3.由于最终双向链表的遍历结果就是二叉搜索树中序的遍历结果;
4.开始中序线索化二叉树(即改变二叉树指针指向)
如果对中序线索化二叉树还有疑问,请看下图:
如图叶子节点的左右孩子指针指向都按中序线索的方式改变了;
4.看代码说话:
第一部分:
首先需要保存最后双向链表的头,即二叉树的最左节点:
Node* _BinaryToDoubleList(Node* root)
{
//1.找到双向链表的头;
Node* head = root;
while(head->_left != nullptr)
{
head = head->_left;
}
Node* prev = nullptr;
_Change(root,prev); //转换函数
return head;
}第二部分:
转换函数:一个递归过程,按照中序线索化走的
void _Change(Node* cur,Node*& prev)
{
if (cur == nullptr)
return;
//1.找到最左边
_Change(cur->_left,prev);
cur->_left = prev; //此时prev为空
if (prev != nullptr)
prev->_right = cur;
prev = cur;
_Change(cur->_right, prev);
}完整测试代码:
#pragma once
template<class K, class V>
struct SBTNode
{
K key;
V value;
SBTNode<K, V> *_left;
SBTNode<K, V> *_right;
SBTNode(const K& key, const V& value)
:key(key)
, value(value)
, _left(nullptr)
, _right(nullptr)
{}
};
template<class K, class V>
class SBTree
{
typedef SBTNode<K, V> Node;
public:
SBTree()
:_root(nullptr)
{}
~SBTree()
{}
public:
//非递归插入
bool Insert(const K& key, const V& value)
{
return _Insert(key, value);
}
//递归插入
bool Insert_R(const K& key, const V& value);
//非递归查找节点
SBTNode<K, V>* Find(const K& key)
{
if (_root == nullptr)
{
return nullptr;
}
SBTNode<K, V> *cur = _root;
while (cur->_left || cur->_right)
{
if (cur->key == key)
{
return cur;
}
else if (cur->key > key)
{
cur = cur->_left;
}
else if (cur->key < key)
{
cur = cur->_right;
}
else
{
return nullptr;
}
}
}
bool _Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new SBTNode<K, V>(key, value);
return true;
}
SBTNode<K, V> *parent = nullptr; //指向cur 的前驱
SBTNode<K, V> *cur = _root;
while (cur)
{
if (cur->key > key) //插左边
{
parent = cur;
cur = cur->_left;
}
else if (cur->key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
if (parent->key < key)
{
SBTNode<K, V> *node = new SBTNode<K, V>(key, value);
parent->_right = node;
return true;
}
else if (parent->key > key)
{
SBTNode<K, V> *node = new SBTNode<K, V>(key, value);
parent->_left = node;
return true;
}
else
{
return false;
}
}
Node* BinaryToDoubleList()
{
return _BinaryToDoubleList(_root);
}
Node* _BinaryToDoubleList(Node* root)
{
//1.找到双向链表的头;
Node* head = root;
while(head->_left != nullptr)
{
head = head->_left;
}
Node* prev = nullptr;
_Change(root,prev); //转换函数
return head;
}
void _Change(Node* cur,Node*& prev)
{
if (cur == nullptr)
return;
//1.找到最左边
_Change(cur->_left,prev);
cur->_left = prev; //此时prev为空
if (prev != nullptr)
prev->_right = cur;
prev = cur;
_Change(cur->_right, prev);
}
//中序遍历
void InOrder(SBTNode<K, V>* root)
{
if (root == nullptr)
{
return; //递归结束出口
}
SBTNode<K, V> *cur = root;
InOrder(cur->_left);
cout << cur->key << " ";
InOrder(cur->_right);
}
//顺序遍历双向链表
void TreaveList()
{
Node* cur = BinaryToDoubleList();
while (cur)
{
cout << cur->key<< " ";
cur = cur->_right;
}
cout << endl;
}
public:
SBTNode<K, V> *_root;
};画图不容易,帮顶,赐教!