lightoj1385 - Kingdom Division
| PDF (English) | Statistics | Forum |
| Time Limit: 1 second(s) | Memory Limit: 32 MB |
The king of Geometry-Land was in deep trouble. His three sons quarrel all the time. The king tried a lot but in vain. "How about dividing the kingdom?" the king thought to himself. So, he called the advisors and described his plan. They opened the map...
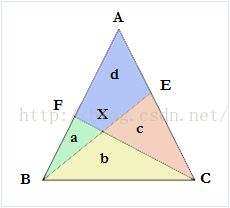
The kingdom is triangular. The king denoted the three vertices as A, B, C. He drew a line from B to E (E is any point in segment AC) and another line from C to F (F is any point in segment AB). The intersection of BE and CF was denoted by X.
Then they got four parts - a (triangle BFX), b (triangle BCX), c (triangle CEX) and d (quadrilateral AEXF). The king decided to give these areas - a, b, c to his three sons. And the area d would be the king's new kingdom.
Now, you are given the value of a, b and c. You have to find the area of d.
Input
Input starts with an integer T (≤ 1000), denoting the number of test cases.
Each case starts with a line containing three positive real numbers a b and c which are not greater than 1000. You can also assume that the numbers contain at most four places after the decimal point.
Output
For each case, print the case number first. Then if the area of d cannot be determined, print "-1". Otherwise print the area of d. Errors less than 10-6 will be ignored.
Sample Input |
Output for Sample Input |
| 4 1 2 1 2 4 2 1 3 3 1.28 2.67 3.12 |
Case 1: 2 Case 2: 4 Case 3: 5 Case 4: 12.4063611138 |
连接EF设AEF面积为y,EFX面积为x考虑b与c同底且高相同,a与x同底且高相同且底边均为BF所以有比例关系a/b=x/c,同理考虑ABF 与BCF同底且高相同,AEF与EFC同底且高相同所以且底均相同所以有比例关系(a+x+y)/(b+c)=(y)/(x+c);
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<list>
#include<vector>
#define eps 1e-6
using namespace std;
int main()
{
int t,test=1;
double a,b,c;
scanf("%d",&t);
while(t--){
scanf("%lf%lf%lf",&a,&b,&c);
double x=a/b*c;
printf("Case %d: ",test++);
if(b-x<eps){
printf("-1\n");
}
else {
double y=(x+c)*(a+x)/(b-x);
printf("%.7lf\n",x+y);
}
}
return 0;
}