赫夫曼编码的应用
blog.sina.com.cn/s/blog_a00f562701018vt2.html
2.1设计要求
本设计要求是对输入的一串电文字符实现赫夫曼编码,再对赫夫曼生成的代码串进行译码,输出电文字符串。
2.2设计分析
利用赫夫曼树求得的用于通信的二进制编码称为赫夫曼编码。树中从根到每个叶子都有一条路径,对路径上的各分支约定:指向左子树的分支表示“0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为和各个叶子对应的字符的编码。根据设计要求和分析,要实现本设计,必须实现以下几个方面的功能:
<1>赫夫曼树的建立;
<2>赫夫曼编码的生成;
<3>编码文件的译码;
2.3算法实现
ⅰ赫夫曼树的建立(存为jlhfms.h文件)
要实现赫夫曼树算法,首先要实现在HT[1…k]中选择parent为0且权值最小的两个根节点的选择算法;另外,还要有一个实现统计输入电文字符串中各种字符出现的频率以及字符的种类的算法。
<1>选择parent为0且权值最小的两个根节点的算法
具体实现代码:
//用户接口
void select(HuffmanTree T,int k,int &s1,int &s2){
//在HT[1....k]中选择parent为0且权值最小的两个根节点
//其序号分别为s1和s2
int i,j;
int min1=101;
for(i=1;i<=k;i++){
if(T[i].weight
j=i;
min1=T[i].weight;
}
}
s1=j; //取得最小权值的编号
min1=32767;
for(i=1;i<=k;i++){
if(T[i].weight
j=i;
min1=T[i].weight;
}
}
s2=j;//取得第二小权值的编号
}
<2>统计字符串中字符的种类以及各类字符的个数
假设电文字符串全是大写字母,那么该算法的实现思想是:先定义一个含有26个元素的临时整型数组,用来存储各种字母出现的次数。因为大写字母的ASCII码与整数1-26之间相差64,因此在算法中使用字母减去64作为统计数组的小标对号入座无需循环判断来实现,从而提高了效率;另外,要求出电文字符串中有多少种字符,并保存这些字符以供编码时使用。统计和保存都比较容易,用一个循环来判断先前统计好的各类字符的个数的数组元素是否为零,若不为零,则将其值存入一个数组对应的元素中,同时将其对应的字符也存入另一个数组的元素之中。
具体实现代码为:
int jsq(char *s,int cnt[],char str[]){
//统计字符串中各种字母的个数以及字符的种类
char *p;
int i,j,k;
//temp[k]数组巧妙地将字符以及该字符出现的次数成功的映射,
//k映射为字符在26个大写字符中的位置,temp[k]的值表示该字符出现的次数
int temp[27];
for(i=1;i<=26;i++){
temp[i]=0;
}//初始化
for(p=s;*p!='\0';p++){
//统计各种字符的个数
if(*p>='A'&&*p<='Z'){
k=*p-64;
temp[k]++;
}
if(*p>='a'&&*p<='z'){
k=*p-96;
temp[k]++;
}
if(*p>='0'&&*p<='9'){
k=*p-47;
temp[k]++;
}
//printf("%c",*s);
//printf("\n");
}
j=0;
i=1;
//str[0]='1';
//printf("%s",s);
if(*s>='A'&&*s<='Z'){
for(i=1,j=0;i<=26;i++){
if(temp[i]!=0){
j++; //j保存字符的个数
str[j]=i+64; //送对应的字母到数组str[]中
cnt[j]=temp[i]; //存入对应字母的权值到数组cnt[]中
}
//printf("%c,权值=%d\n",str[j],cnt[j]);
}
}
if(*s>='0'&&*s<='9'){
for(i=1,j=0;i<=26;i++){
if(temp[i]!=0){
j++; //j保存字符的个数
str[j]=i+47; //送对应的字母到数组str[]中
cnt[j]=temp[i]; //存入对应字母的权值到数组cnt[]中
//printf("%c,权值=%d\n",str[j],cnt[j]);
}
}
}
if(*s>='a'&&*s<='z'){
for(i=1,j=0;i<=26;i++){
if(temp[i]!=0){
j++; //j保存字符的个数
str[j]=i+96; //送对应的字母到数组str[]中
cnt[j]=temp[i]; //存入对应字母的权值到数组cnt[]中
//printf("%c,权值=%d\n",str[j],cnt[j]);
}
}
}
return j;
}
<3>构造赫夫曼树
具体实现代码为:
void ChuffmanTree(HuffmanTree HT,HuffmanCode HC,int cnt[],char str[]){
//构造哈夫曼树
int i,s1,s2;
for(i=1;i<=2*num-1;i++){
//初始化HT
HT[i].lchild=0;
HT[i].rchild=0;
HT[i].parent=0;
HT[i].weight=0;
}
for(i=1;i<=num;i++){
//输入num个叶节点的权值
HT[i].weight=cnt[i];
}
for(i=num+1;i<=2*num-1;i++){
//在HT{1....i-1]中选择parent为0且权值最小的两个根节点
//其序号分别为s1和s2,并依次生成新节点
select(HT,i-1,s1,s2);
HT[s1].parent=i;
HT[s2].parent=i;
HT[i].lchild=s1;
HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
for(i=1;i<=num;i++){
//输入字符集中的字符
HC[i].ch=str[i];
}
i=1;
printf("\n\n");
while(i<=num){
printf("字符%c,次数为:%d\n",HC[i].ch,cnt[i++]);
}
}
ⅱ赫夫曼编码
<1>定义数据类型:(存为nodetype.h文件)
#include
#include
#define n 100 //叶子节点数
#define m 2*n-1 //哈夫曼树中节点总数(包括新生成的n-1个节点)
typedef struct{
char ch; //待编码的字符
char bits[9]; //存放编码位串(为什么大小设置为9?)
int len; //编码长度
}CodeNode;
typedef CodeNode HuffmanCode[n+1]; //待编码的n-1个字符
typedef struct{
int weight; //权值
int lchild,rchild,parent; //左右孩子及双亲指针
}HTNode; //树中节点类型
typedef HTNode HuffmanTree[m+1]; //0号单元不用(共有m个节点,在哈夫曼编码时新生成的节点也对需要编码的字符产生影响)
int num; //num定义为全局变量,用来存储待编码的字符个数
<2>赫夫曼编码算法:(存为scbmwj.h文件)
void HuffmanEncoding(HuffmanTree HT,HuffmanCode HC){
//根据哈夫曼树HT求哈弗曼编码表HC
int c,p,i; //c和p分别指示T中孩子和双亲的位置
char cd[n]; //临时存放编码串
int start; //指示编码在cd中的起始位置
cd[num]='\0'; //最后一位放上串结束符
for(i=1;i<=num;i++){
start=num; //初始位置
c=i; //从叶子节点T[i]开始上溯
p=HT[c].parent;
while((p=HT[c].parent)>0) {
//直至上溯到HT[c]是树根为止
//若T[c]是T[p]的左孩子,则生成0,否则生成代码1
cd[--start]=(HT[p].lchild==c)?'0':'1';
c=p;
}
strcpy(HC[i].bits,&cd[start]);
HC[i].len=num-start;
printf("%c: %s\n",HC[i].ch,HC[i].bits);
}
}
<3>建立正文的编码文件(存在scbmwj.h文件中)
基本思想是:将要编码的字符串中的字符逐一与预先生成赫夫曼树时保存的字符编码对照表惊醒比较,找到之后,对该字符的编码写入代码文件,直至所有的字符处理完为止,具体实现算法:
void coding(HuffmanCode HC,char *str){
//对str所代表的字符串进行编码,并写入文件
int i,j;
FILE *fp;
fp=fopen("codefile.txt","w");
printf("\n\n输入的字符文件编码为:\n");
while(*str){
for(i=1;i<=num;i++){
if(HC[i].ch==*str){
for(j=0;j
fputc(HC[i].bits[j],fp);
printf("%c",HC[i].bits[j]);
}
printf("●");
break;
}
}
str++;
}
fclose(fp);
}
ⅲ代码文件的译码(存为dwym.h文件)
译码的基本思想是:读文件中的编码,并与原生成的赫夫曼编码表比较,遇到相等时,即取出其对应的字符存入一个新串中。
具体实现代码为:
char * decode(HuffmanCode HC){
//代码文件codefile.txt的译码
FILE *fp;
char str[254]; //假设原文本文件不超过254个字符
char *p;
static char cd[n+1];
int i,j,k=0,cjs;
fp=fopen("codefile.txt","r");
while(!feof(fp)){
cjs=0;
for(i=0;i
cd[i]=' ';
cd[i+1]='\0';
cd[i]=fgetc(fp);
for(j=1;j<=num;j++){
if(strcmp(HC[j].bits,cd)==0){
str[k]=HC[j].ch;
k++;
cjs=1;
break;
}
}
}
}
str[k]='\0';
p=str;
return p;
}
2.4程序代码
#include
#include
#include
#include"nodetype.h"
#include"jlhfms.h"
#include"scbmwj.h"
#include"dwym.h"
//入口函数
void main(){
char st[254],*s,str[27];
int i;
int cn[27];
HuffmanTree HT;
HuffmanCode HC;
printf("输入需要编码的字符串(假设均为大写字母或者均为数字):\n");
gets(st); //将字符串存入到st[]里面
for(i=0;st[i]!='\0';i++){
//if(st[i]<'A'||st[i]>'Z'){
// printf("请保证输入的字符都是大写字母!\n");
//exit(0);
// }else{
num=jsq(st,cn,str); //统计字符的种类以及各字符出现的频率
//}
}
ChuffmanTree(HT,HC,cn,str); //建立哈夫曼树
printf("\n\n字符对应的哈夫曼编码为:\n");
HuffmanEncoding(HT,HC);
coding(HC,st); //建立电文哈弗曼编码文件
s=decode(HC); //读编码文件译码
printf("\n\n译码后的字符串:\n");
printf("%s\n\n",s); //输出译码后的字符串
}
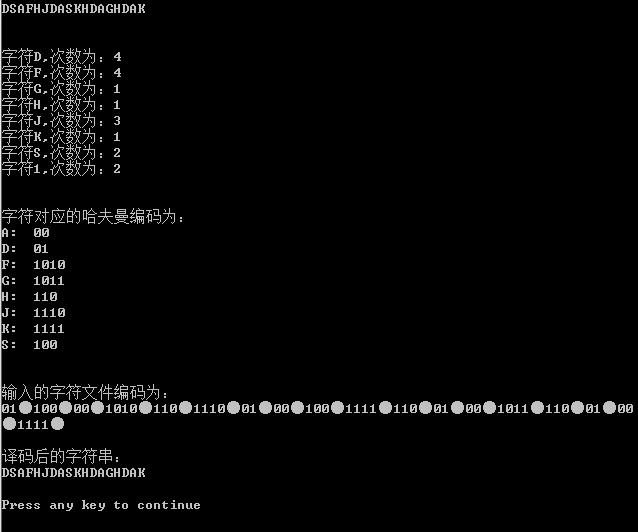
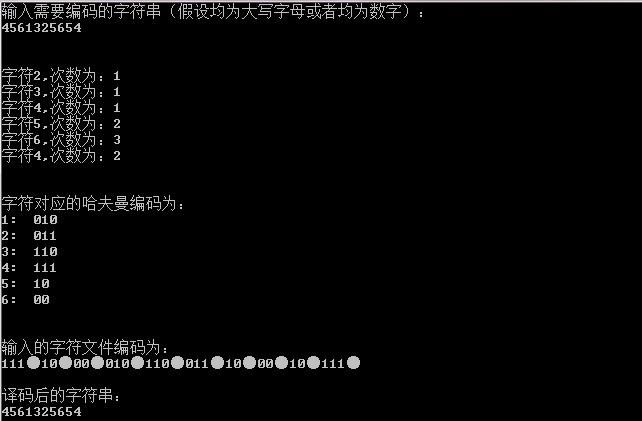
2.5测试结果
2.6结论分析
以二叉链表作为存储结构,对二叉树的遍历及赫夫曼树、赫夫曼编码等概念进行综合练习,探讨各种非递归的遍历算法以及求根节点到任意结点的路径。赫夫曼编码的实现,综合了二叉树的各种运用,以及对以后压缩技术也提供了一定的指引,这次设计在原有功能的基础上也实现了对数字的编码,但后来想想,对数字编码是否存在实际意义,这也是做完后自己的一点思考。