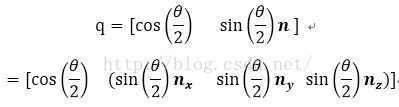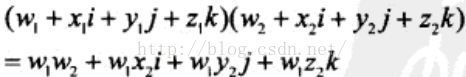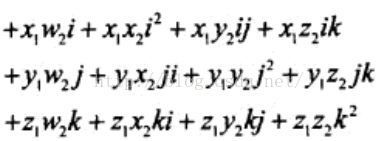球面线性插值(Spherical Linear Interpolation,Slerp)
参考文献:http://blog.csdn.net/pizi0475/article/details/7918314以及《3D数学基础:图形与游戏开发》
实例:
问题:3D空间中,在等长度的两个交角为theta的向量V1(x1,y1,z1)和V2(x2,y2,z2)。
实例:行星绕太阳转动,找到旋转过程的两个位置p1,p2,现在模拟从p1到p2的过程。
思路:
1. 一般线性插值
线性插值方法:
这里可以看出,插值的部分就是向量V3.下面来证明V3与t的关系V2-V1得到V1指向V2的向量,再乘以t就是V1指向V3的向量了,最后加上向量V1就是向量V3了,公式为:
v(t) = v1 + t*(v2-v1)(0<=t<=1)(因为t是一次方的,所以是线性的。)
【注:可以看出一般线性插值长度变化了,不满足要求,用球面线性插值就不会变化。】
2. 一般球面线性插值
将插值结果放大一个放大系数k(t),使其长度放大到|v1|或者|v2|(简单的说就是保持长度不变)。
v(t) = k(t)*(v1 + t*(v2-v1))
其中k(t) =|v1|/|v(t)|=|v1|/|v1+t*(v2-v1)|.
这样,插值向量v(t)的端点就会沿着v1,v2端点构成的圆弧进行。v1和v2是等长的,圆弧实际位于v1和v2构成的曲面上的一段。所以又叫球面线性插值。
这个插值解决了3D空间中旋转的插值,在关键帧动画中可以用来计算两个关键帧之间的动画。但是,由于它的插值不是等角速度的,而是变速的。所以如果用来实现案例中的效果的话还需进一步处理。
【注】一般球面线性插值v(t)与v1的夹角theta(t)不是t的线性函数。
证明过程如下:
3. 改进的球面线性插值,有两种方法:
1> 四元数工具
变换方法:
构造四元数q(cos ,sin *v1’),r(cos ,sin *v2’)(v1’,v2’为单位v1,v2向量),以及参数t(0≤t≤1),则构造四元数变换:
a. 四元数s(w,v’)=r*(q-1)t*q即为球面线性插值变换。其中,s的虚部v1’和v2’间的插值向量,乘以长度![]() ,即得v1,v2间插值向量v。
,即得v1,v2间插值向量v。
b. 另一种变形形式是对四元数进行插值变换
s(w,v’)=a*q+b*r
其中a=sin(α(1-t))/sinα,b=sin(α*t)/sinα,cosα=x1*x2+y1*y2+z1*z2+w1*w2
S的虚部v’即为v1’和v2’间的插值向量,乘以长度 ![]() ,即得v1,v2间插值向量v。
,即得v1,v2间插值向量v。
2> 利用旋转矩阵
变换方法:v=v1*Trot
其中,Trot即绕任意轴旋转的矩阵变换矩阵,因为v1到v2间的插值可以看成是v1绕垂直于v1,v2组成的平面的向量的旋转,所以实际上是绕轴旋转的问题,不过相应参数变成 =t*θ,轴q(q1,q2,q3)变成向量
对于四元数插值:
四元数的记法:
一个标量w和一个3D向量分量v或者(x,y,z),两种记法分别如下:
[w,v]或者[w,(x,y,z)]
四元数定义了三个虚部i,j,k,它们之间的关系如下:
一个四元数[w,(x,y,z)]定义了一个复数![]()
四元数与轴—角对
n为旋转轴,θ为绕轴旋转的量,因此(n, θ)定义了一个角位移:绕n指定的轴旋转θ角
n、θ不能直接存储在四元数的四个数中,它们在四元数里,但是不是这么直接,四元数中的数与n、θ的关系如下:
四元数求负
四元数的求负是对每个分量变负就可以了,即-q=-[w,(x,y,z)]=[-w,(-x,-y,-z)]=-[w,v]=[-w,-v]
但是q和-q表示的角位移是相同的,原因可以参看轴角对,当旋转角θ为360°或其倍数时,不会改变q的角位移,但是q的四个分量都变负了
四元数的叉乘
叉乘是由四元数的复数形式推导出来的:
这就推出了四元数乘法的标准定义
四元数的点乘
四元数点乘的绝对值越大,a和b代表的角位移越相似。
四元数的差:
‘差’被定义为一个方位到另一个方位的角位移。也就是说给定方位a和b,能够计算从a旋转到b的角位移d。用四元数表示为ad=b。得出d=a-1b
四元数求幂:
四元数求幂可以从角位移中抽取“一部分”。例如q代表一个角位移,q1/3就代表1/3这个角位移的四元数。
为了理解上式的各个参数,我们重新定义了四元数,引入一个新变量α=θ/2
q的对数定义为下式:
设四元数p的形式为[0 , αn],n为单位向量
p=[0, αn]=[0 ,(αx,αy,αz)] ||n||=1
四元数的指数
四元数求幂的C++程序
注意,w=1或者﹣1都会导致mult计算除零现象,acos函数返回的是正的角度。
四元数插值:
当前四元数比较重要的一个用途就是球面线性插值(Spherical Linear Interpolation),可以在两个四元数之间平滑插值。
插值步骤:
① 计算两个值的差:q0到q1的角位移由△q=q0-1q1给出
② 计算差的一部分。四元数求幂可以做到。差的一部分由△qt给出
③ 在开始值上加上差的一部分,用四元数乘法组合角位移q0△qt
这样就可以得到slerp公式:
以上是理论上的计算方法,下面介绍一个更加有效的方法。
Slerp的思想就是沿着4D球面上连接两个四元数的弧插值。
先看平面上的两个2D向量v0和v1都是单位向量,我们需要计算vt它是沿着v0到v1弧的平滑插值。设w是v0到vt弧所截的角,那么vt就是v1沿弧旋转tw的结果。
需要考虑两点问题:一是四元数q和-q代表同一方位,但是作为slerp的参数时,可能有不一样的结果,是因为4D球面不是欧式空间的直接扩展,而这种现象在2D 3D空间是不会发生的。解决方法是选择q0和q1的符号使得点乘q0.q1的结果是非负。第二就是如果q0和q1非常接近,sinθ会非常小,这时除法会出现问题。解决方法是此时采用线性插值。
matlab实现的球面线性插值:
SlerpInsert.m
function r= SlerpInsert(p,q,t)
%球面线性插值
%程序考虑了p、q点乘结果为负的情况
%返回的插值结果是r
w0=p(1);
x0=p(2);
y0=p(3);
z0=p(4);
w1=q(1);
x1=q(2);
y1=q(3);
z1=q(4);
%用点乘计算两个四元数夹角的cos值
cosOmega=w0*w1+x0*x1+y0*y1+z0*z1;
%如果点乘为负,则反转一个四元数以取得短的4D弧
if(cosOmega<0.0)
w1=-w1;
x1=-x1;
y1=-y1;
z1=-z1;
cosOmega=-cosOmega;
end
%检查他们是否接近,以避免除零
if cosOmega>0.99999999 %cos=1的时候就是夹角为0,重合
k0=1.0-t;
k1=t;
else
%用三角公式sin?+cos?=1计算sin值
sinOmega=sqrt(1.0-cosOmega*cosOmega);
%通过sin和cos计算角度
omega=atan2(sinOmega,cosOmega) %计算点(cosOmega,sinOmega)与x轴正向的夹角
%计算分母的倒数,这样就只需要一次除法
oneOverSinOmega=1.0/sinOmega;
%计算插值变量
k0=sin((1.0-t)*omega)*oneOverSinOmega;
k1=sin(t*omega)*oneOverSinOmega;
end
%插值
w=w0*k0+w1*k1;
x=x0*k0+x1*k1;
y=y0*k0+y1*k1;
z=z0*k0+z1*k1;
r(1)=w;r(2)=x;r(3)=y;r(4)=z;
end
test.m
q=[1 2 3 4] p=[1 3 6 8]; SlerpInsert(p,q,0.5)
结果:
r =
1.0000 2.5000 4.5000 6.0000
对于球面线性插值的立体演示,在后续文章中会给出代码~~