ZOJ 3328 Wu Xing

Wu Xing Time Limit: 1 Second       Memory Limit: 32768 KB

Introduction

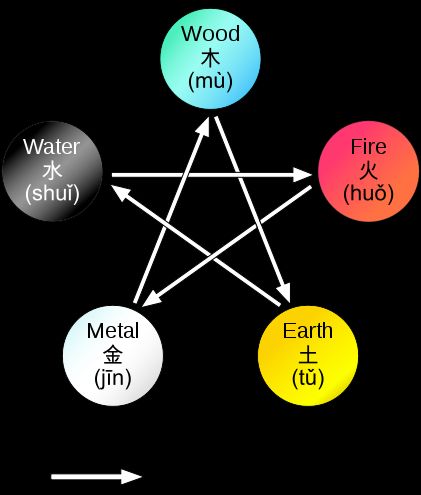
The Wu Xing, or the Five Movements, Five Phases or Five Steps/Stages, are chiefly an ancient mnemonic device, in many traditional Chinese fields.

The doctrine of five phases describes two cycles, a generating or creation cycle, also known as "mother-son", and an overcoming or destruction cycle, also known as "grandfather-nephew", of interactions between the phases.

Generating:

• Wood feeds Fire;
• Fire creates Earth (ash);
• Earth bears Metal;
• Metal carries Water (as in a bucket or tap, or water condenses on metal);
• Water nourishes Wood.

Overcoming:

• Wood parts Earth (such as roots) (or Trees can prevent soil erosion );
• Earth absorbs (or muddies) Water (or Earth dam control the water);
• Water quenches Fire;
• Fire melts Metal;
• Metal chops Wood.

With the two types of interactions in the above graph, any two nodes are connected by an edge.

Problem

In a graph with N nodes, to ensure that any two nodes are connected by at least one edge, how many types of interactions are required at least? Here a type of interaction should have the following properties:

• It can be represented as a set of directed edges in the graph.
• For each type of interaction, there should be one and only one edge starting at each node.
• For each type of interaction, there should be one and only one edge ending at each node.
• The interactions are made up of cycles, i.e. starting from an arbitrary node and following the edges with the same type of interaction, you can always reach the starting node after several steps.

Input

For each test case, there's a line with an integer N (3 <= N < 1,000,000), the number of nodes in the graph.

N  = 0 indicates the end of input.

Output

For each test case, output a line with the number of interactions that are required at least.

Sample Input

5
0

Sample Output

2

Reference

http://en.wikipedia.org/wiki/Wu_Xing

题目大意：有n个顶点的有向图，每两个顶点之间都有一条边。给出interaction的定义『1、这是一个有向边集；2、有且仅有一条开始边；3、有且仅有一条结束边；4、最后成环』，问最少有多少个interaction，就能把图全覆盖。


题目分析：以下分析建立在一个基础上，每一笔都能画出一个n条边的环（而事实似乎就是如此）。我们可以看到，他说要是任意两个点都有联系，看到这里，马上可以想到，要满足这个条件， 必须需要n*(n-1)/2条边，于是，换一种思考，该题目就可以理解为，在n*（n-1）/2条边中可以构成几个环。如果想到这里，你又开始去画点画边，那估计最后结果还是要悲剧。至少我是画不出，就算画出了也不知道到底是否是最小个数的环。 所以我们接着继续分析。。。抛开怎么连线不管， 往整体方向想，要构成一个环， n个点必须要n条边，可以理解，最终所有环所构成的边，都不会超过n*（n-1）/2条边。 所以每条边都在一个或几个环内，（其中不同的环可以共用一条边）。 所以至少有（n-1）/2个环， 如果可以整除，那么商就是答案。如果不能整除呢？ 那么余下的边必定可以再组成一个环。所以如果（n-1）%2 != 0, 那么答案就等于（n-1）/2 +1;结果就是和n/2的结果一样

#include<stdio.h>  
int main()  
{  
    int n;  
    while(scanf("%d",&n),n)  
        printf("%d\n",n/2);  
    return 0;  
}