nyoj-711最舒适的路线
这道题我也是看了别人的解题思路才会做了。
对于一个分数a/b(a>b),要使a/b最小,使a-b很小,相同a-b的情况下,a,b值越大的越小。
所以这个枚举就从按最大的边降序排列。不断的添加边直到s,t连通。判断连通就使用并查集。
for(i=0;i<m;i++)
{
init();
for(j=i;j<m;j++)
{
if(!same(g[j].from,g[j].to))
unite(g[j].from,g[j].to);
if(same(s,t))
break;
}
if(j==m)
break;
int mx=g[i].speed,mn=g[j].speed;
// printf("%d %d\n",mx,mn);
if(mx*1.0/mn<rmx*1.0/rmn)
{
rmx=mx;rmn=mn;
}
}
最后添加的边肯定是在s->t的路径上,肯定是最小的。但是前面添加的边不一定是有效的。
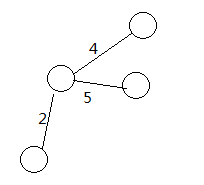
比如这种情况。权值为5的边是最先添加的,但是它不在s->t的路径上。
所以mx=g[i].speed是假设当前边为有效的最大值的边。随着i的推进,就会排除无效的边。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define Max_E 5100
#define Max_V 510
#define INF 0x3f3f3f3f
struct Edge{
int from,to,speed;
}g[Max_E];
int par[Max_V];
int rank[Max_V];
int n,m;
int s,t;
int cmp(const void *a,const void *b)
{
return ((Edge *)b)->speed-((Edge *)a)->speed;
}
void init()
{
for(int i=0;i<=n;i++)
{
par[i]=i;
rank[i]=0;
}
}
int find(int x)
{
if(par[x]==x)
return x;
return par[x]=find(par[x]);
}
void unite(int x,int y)
{
x=find(x);
y=find(y);
if(x==y)
return;
if(rank[x]<rank[y])
par[x]=y;
else
{
par[y]=x;
if(rank[x]==rank[y])
rank[x]++;
}
}
bool same(int x,int y)
{
return find(x)==find(y);
}
int main()
{
int K;
int i,j;
scanf("%d",&K);
while(K--)
{
scanf("%d%d",&n,&m);
for(i=0;i<m;i++)
{
scanf("%d%d%d",&g[i].from,&g[i].to,&g[i].speed);
}
scanf("%d%d",&s,&t);
qsort(g,m,sizeof(g[0]),cmp);
/*for(i=0;i<m;i++)
printf("%d ",g[i].speed);*/
int rmx=INF,rmn=1;
for(i=0;i<m;i++)
{
init();
for(j=i;j<m;j++)
{
if(!same(g[j].from,g[j].to))
unite(g[j].from,g[j].to);
if(same(s,t))
break;
}
if(j==m)
break;
int mx=g[i].speed,mn=g[j].speed;
// printf("%d %d\n",mx,mn);
if(mx*1.0/mn<rmx*1.0/rmn)
{
rmx=mx;rmn=mn;
}
}
if(rmx==INF)
{
printf("IMPOSSIBLE\n");
continue;
}
int l=2;
while(l<=rmn)
{
if(rmx%l==0&&rmn%l==0)
{
rmx/=l;rmn/=l;
}
else l++;
}
if(rmn==1)
printf("%d\n",rmx);
else printf("%d/%d\n",rmx,rmn);
}
return 0;
}