K-means聚类算法
相关概念
无监督学习
我们前面所学的逻辑回归,线性回归等都需要经过 Traindata 的训练,而无监督学习与我们前面所讲的不同,无监督学习的目的是学习出一个function f ,包括两种:
- 密度估计(density estimation)
- 聚类(clustering)
聚类
聚类顾名思义就是将数据分为多少类,或者给出没一类的概率,不需要提前进行训练,聚类算法就是无监督学习最常见的一种,给定一组数据, 需要聚类算法去发掘数据中的隐藏结构。
通过这张图对聚类有个初步的认识。

K-means算法
K-means算法的流程
初始数据 {x(1),...,x(m)} , x(i)∈Rn
Step1:
选取k个聚类重心 μ1,...,μk , μi∈Rn
样本中心初始化的方法:
从样本中随机选择 k 个使 μi 等于它们,然后随机初始化(50~1000次)选择最优的。
Step2:

Step3:

Step4:
重复第二步第三步直到聚类中心的变化低于阀值。
在聚类结束后,如果一个中心没有得到任何样本,那么需要去除这个中心点,或者重新 初始化。
分类中心个数K的选择
肘部法则:
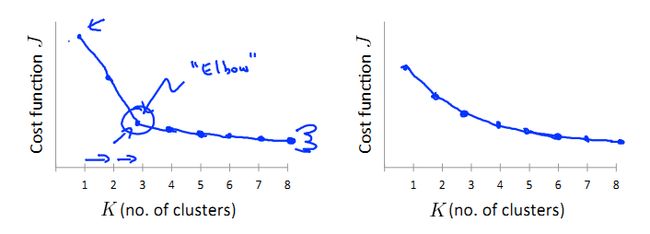
从左图中可以直观的看出在某一点 J(label,μ) 发生了明显的转折,我们将转折点称为肘部,那么我们就可以选择该点的k值作为K。
但是大多数情况 J(label,μ) 随K的变化图像都如右图没有明显的肘部,那么我们就需要根据实际情况具体分析。
MatlabCode
随机初始化聚类中心
Code
function centroids = kMeansInitCentroids(X, K)
%KMEANSINITCENTROIDS This function initializes K centroids that are to be
%used in K-Means on the dataset X
% centroids = KMEANSINITCENTROIDS(X, K) returns K initial centroids to be
% used with the K-Means on the dataset X
%
% You should return this values correctly
centroids = zeros(K, size(X, 2));
% ====================== YOUR CODE HERE ======================
% Instructions: You should set centroids to randomly chosen examples from
% the dataset X
%
randidx = randperm(size(X, 1));
centroids = X(randidx(1:K), :);
% =============================================================
end
将点分类,求 label(i)
Code
function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
% idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
% in idx for a dataset X where each row is a single example. idx = m x 1
% vector of centroid assignments (i.e. each entry in range [1..K])
%
% Set K
K = size(centroids, 1);
% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Go over every example, find its closest centroid, and store
% the index inside idx at the appropriate location.
% Concretely, idx(i) should contain the index of the centroid
% closest to example i. Hence, it should be a value in the
% range 1..K
%
% Note: You can use a for-loop over the examples to compute this.
%
for i=1:size(X,1)
idx(i)=1;
for j =1:K
if norm(X(i,:)-centroids(idx(i),:)) > norm(X(i,:)-centroids(j,:))
idx(i)=j;
end;
end;
end;
% =============================================================
end
更新聚类中心
Code
function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returs the new centroids by computing the means of the
%data points assigned to each centroid.
% centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by
% computing the means of the data points assigned to each centroid. It is
% given a dataset X where each row is a single data point, a vector
% idx of centroid assignments (i.e. each entry in range [1..K]) for each
% example, and K, the number of centroids. You should return a matrix
% centroids, where each row of centroids is the mean of the data points
% assigned to it.
%
% Useful variables
[m n] = size(X);
% You need to return the following variables correctly.
centroids = zeros(K, n);
% ====================== YOUR CODE HERE ======================
% Instructions: Go over every centroid and compute mean of all points that
% belong to it. Concretely, the row vector centroids(i, :)
% should contain the mean of the data points assigned to
% centroid i.
%
% Note: You can use a for-loop over the centroids to compute this.
%
for i=1:K
list = find(idx==i);
for j=1:size(list,1)
centroids(i,:)=centroids(i,:)+X(list(j),:);
end;
centroids(i,:)=centroids(i,:)./size(list,1);
end;
% =============================================================
end
RunK-means
Code
function [centroids, idx] = runkMeans(X, initial_centroids, ...
max_iters, plot_progress)
%RUNKMEANS runs the K-Means algorithm on data matrix X, where each row of X
%is a single example
% [centroids, idx] = RUNKMEANS(X, initial_centroids, max_iters, ...
% plot_progress) runs the K-Means algorithm on data matrix X, where each
% row of X is a single example. It uses initial_centroids used as the
% initial centroids. max_iters specifies the total number of interactions
% of K-Means to execute. plot_progress is a true/false flag that
% indicates if the function should also plot its progress as the
% learning happens. This is set to false by default. runkMeans returns
% centroids, a Kxn matrix of the computed centroids and idx, a m x 1
% vector of centroid assignments (i.e. each entry in range [1..K])
%
% Set default value for plot progress
if ~exist('plot_progress', 'var') || isempty(plot_progress)
plot_progress = false;
end
% Plot the data if we are plotting progress
if plot_progress
figure;
hold on;
end
% Initialize values
[m n] = size(X);
K = size(initial_centroids, 1);
centroids = initial_centroids;
previous_centroids = centroids;
idx = zeros(m, 1);
% Run K-Means
for i=1:max_iters
% Output progress
fprintf('K-Means iteration %d/%d...\n', i, max_iters);
if exist('OCTAVE_VERSION')
fflush(stdout);
end
% For each example in X, assign it to the closest centroid
idx = findClosestCentroids(X, centroids);
% Optionally, plot progress here
if plot_progress
plotProgresskMeans(X, centroids, previous_centroids, idx, K, i);
previous_centroids = centroids;
fprintf('Press enter to continue.\n');
pause;
end
% Given the memberships, compute new centroids
centroids = computeCentroids(X, idx, K);
end
% Hold off if we are plotting progress
if plot_progress
hold off;
end
end