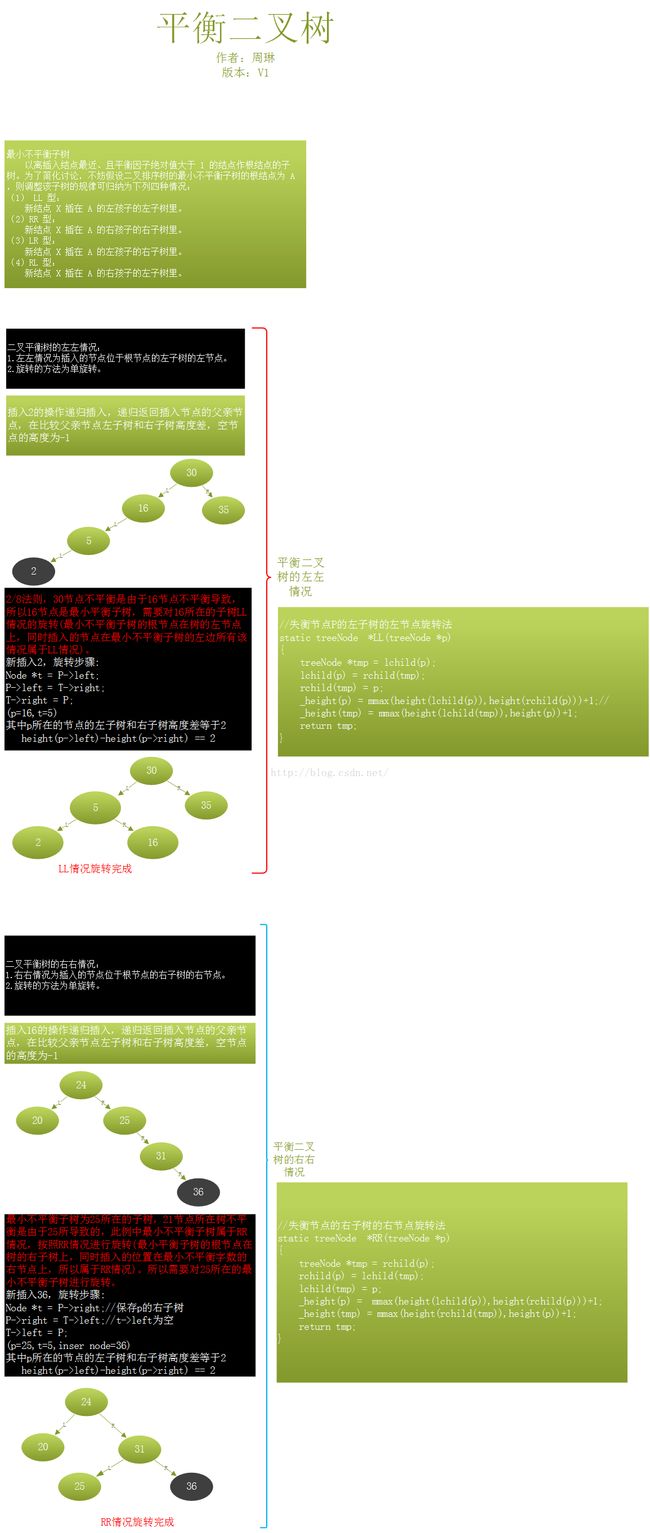
平衡二叉树旋转原理(图示)
/*************************************************************************
> File Name: btree.h
> Author: zhoulin
> Mail: [email protected]
> Created Time: Sat 30 Apr 2016 09:41:43 AM CST
************************************************************************/
#ifndef _BTREE_H
#define _BTREE_H
typedef struct _treeNode
{
int val;
unsigned int height;
struct _treeNode *lchild;
struct _treeNode *rchild;
}treeNode;
typedef struct _treeMgr
{
int count;
struct _treeNode *root;
struct _treeNode *max;
struct _treeNode *min;
}treeMgr;
//---------------------define--------------
#define lchild(T) (T->lchild)
#define rchild(T) (T->rchild)
#define _height(T) (T->height)
#define val(T) (T->val)
#define mmax(M,N) ((M > N)? M:N)
#define root(M) (M->root)
#define tmin(M) (M->min)
#define tcount(M) (M->count)
#define tmax(M) (M->max)
//-------------------operation of tree------------
treeMgr *init();
treeNode *add(int data,treeMgr *m);
treeNode *del(treeMgr *m);
treeNode *findOne(int val,treeMgr *m);
treeNode *prt(treeNode *p,int n);
treeNode *findSmall(treeNode *cur,treeMgr *m);
treeNode *findBig(treeNode *cur,treeMgr *m);
//-----------------------static method-------------
//左左情况
static treeNode *LL(treeNode *p);
//右右单旋转
static treeNode *RR(treeNode *p);
//左右情况
static treeNode *RL(treeNode *p);
//右左情况
static treeNode *LR(treeNode *p);
static int height(treeNode *p);
#endif
/*************************************************************************
> File Name: btree.c
> Author: zhoulin
> Mail: [email protected]
> Created Time: Sat 30 Apr 2016 09:58:50 AM CST
************************************************************************/
#include "btree.h"
#include <stdio.h>
#include <stdlib.h>
//root节点的左子树的左节点旋转法
static treeNode *LL(treeNode *p)
{
treeNode *tmp = lchild(p);
lchild(p) = rchild(tmp);
rchild(tmp) = p;
_height(p) = mmax(height(lchild(p)),height(rchild(p)))+1;//
_height(tmp) = mmax(height(lchild(tmp)),height(p))+1;
return tmp;
}
//root节点的右子树的右节点旋转法
static treeNode *RR(treeNode *p)
{
treeNode *tmp = rchild(p);
rchild(p) = lchild(tmp);
lchild(tmp) = p;
_height(p) = mmax(height(lchild(p)),height(rchild(p)))+1;
_height(tmp) = mmax(height(rchild(tmp)),height(p))+1;
return tmp;
}
//root节点的左子树的右节点旋转法
static treeNode *LR(treeNode *p)
{
lchild(p) = RR(lchild(p));
return LL(p);
}
//root节点的右子树的左节点旋转法
static treeNode *RL(treeNode *p)
{
rchild(p) = LL(rchild(p));
return RR(p);
}
static int height(treeNode *p)
{
if(p == NULL)
return -1;
return _height(p);
}
static treeNode *_add(int data,treeNode *p)
{
if(p == NULL)
{
treeNode *cur = (treeNode *)malloc(sizeof(*cur));
val(cur) = data;
_height(cur) = 0;
lchild(cur) = rchild(cur) = NULL;
p =cur;
}
else if(data < val(p))
{
lchild(p) = _add(data,lchild(p)); //递归调用,返回上一级的父亲节点
if(height(lchild(p)) - height(rchild(p)) == 2){ //判断递归返回的父亲节点的左子树和右子树高度
if(data < val(lchild(p))) //如果插入的值小于当父亲节点的值,说明是插入到的是当前父亲节点子树的左节点上
{
p = LL(p);
}
else
{
p = LR(p); //插入的值在root左子树的右节点上
}
}
}
else if(data > val(p))
{
rchild(p) = _add(data,rchild(p));//递归调用,返回上一级的父亲节点
if(height(rchild(p)) - height(lchild(p)) == 2){
if(data > val(rchild(p)))
{
p = RR(p);//插入的值在右子树的右节点上
}
else
{
p = RL(p);//插入的值在root节点右子树的左节点上
}
}
}
_height(p) = mmax(height(lchild(p)),height(rchild(p)))+1;
return p;
}
treeNode *add(int data,treeMgr *m)
{
treeNode *p = _add(data,root(m));
if(p != NULL){
if(tcount(m) == 0)
{
tmax(m) = tmin(m) = p;
}
if(data <= val(p)){
tmax(m) = p;
}
else{
tmin(m) = p;
}
tcount(m)++;
}
return p;
}
treeMgr *init()
{
treeMgr *m = (treeMgr *)malloc(sizeof(*m));
root(m) = tmax(m) = tmin(m) = NULL;
tcount(m) = 0;
return m;
}
treeNode *prt(treeNode *p,int n)
{
if(p != NULL)
{
int i;
for(i = 0;i <= n;i++)
{
fprintf(stdout," ");
}
fprintf(stdout,"%d[%d]\n",val(p),_height(p));
prt(lchild(p),n+1);
prt(rchild(p),n+1);
}
}
int main(void)
{
int i,n=8;
treeMgr *m = init();
for(i = 1;i <= n;i++ )
{
int v = rand()%1024;
treeNode *p = add(v,m);
root(m) = p;
fprintf(stdout,"val = %d,height=%d\n",val(p),height(p));
}
treeNode *root = root(m);
prt(root,0);
return 0;
}