时间序列 R 读书笔记 04 Forecasting: principles and practice

本章开始学习《Forecasting: principles and practice》

1 getting started

1.1 事件的可预言性

一个时间能不能被预言主要取决于以下三点
1. 对事件的影响因素的了解程度，比如彩票号码，没有内在的影响因素不能被预测
2. 可用数据量的多少，数据量太少没法预测
3. 预测结果本身的影响，比如预测汇率，可能大家知道预测的会长，那么人们就会采取相应的措施使预测结果不准。

1.2 常用预测模型

1. 解释性模型，如其模型内包含其影响因素，通过影响因素来预测属于
2. 时间序列，其模型只用时间来预测
3. 综合模型，即考虑时间也考虑影响因素，不同学科有不同的名字，如，dynamic regression models, panel data models, longitudinal models, transfer function models, and linear system models (assuming ff is linear)

2 工具箱使用

2.1 自相关

使用散点图，画出 Yt 与 Yt−k 的散点图可以看出两者之间的线性关系，自相关系数即能表明他们之间是否有线性关系。
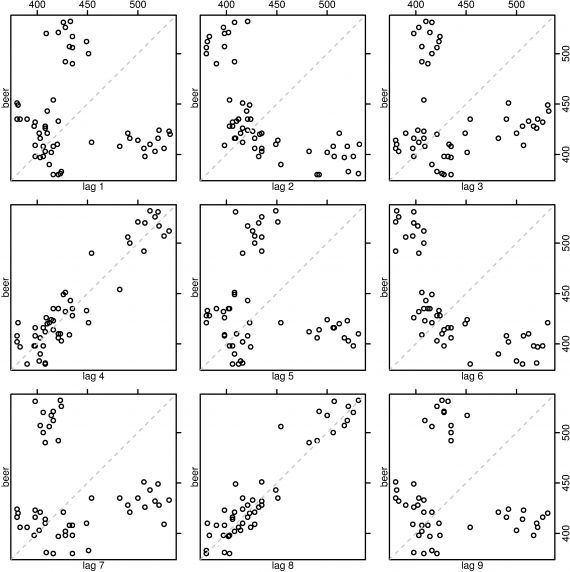
下图是啤酒销量的自相关关系

他们的自相关系数计算公式是：

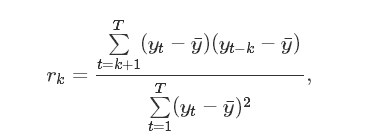
计算结果是：

可以看出在4,8处有较好的正相关，与图相符合
在使用时经常使用ACF来表达，下面是R语言做的图

Acf(beer2)

没有自相关性的就是白噪声，他的ACF如下图

set.seed(30)
x <- ts(rnorm(50))
plot(x, main="White noise")
Acf(x)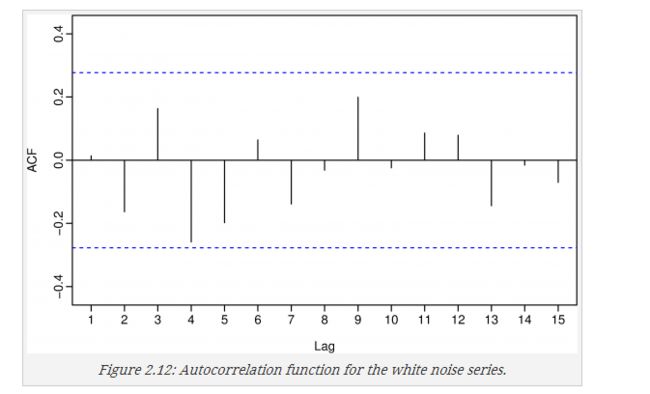

如何通过ACF看是否是白噪声？
通常如果95%的数据的ACF在 ±2T√ 就可以认为是白噪声，这里一共有50个数，ACF的边界是2/（50）^0.5=0.28,所以可以看做是白噪声

2.2 简单模型

1. 平均值模型，直接使用平均值来作为预测值
2. naive模型，直接使用最近的值作为预测
3. 季节naive模型，直接使用最近的季节性数据来作为预测值
4. 飘逸模型，使用历史的平均变化率做线性预测，公式如下：
   
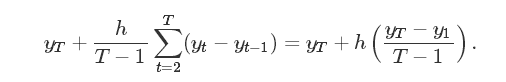
   这几种模型往往不是用来做预测，而是可以用来做预测基准，get√！
   代码如下：

1
meanf(y, h) 
# y contains the time series
# h is the forecast horizon
2
naive(y, h)
rwf(y, h) # Alternative
3
snaive(y, h)
4
rwf(y, h, drift=TRUE)

2.3 转换与调整

2.3.1 数学转化

该类转换一般时将数值的表达形式进行转换，比如转换为log，或者exp形式，文中介绍了一个比较好用的公式，函数为Box-cox

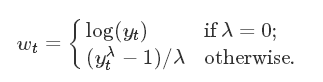
选择合适的 λ 来进行预测，预测之后再将结果转化回正常形式
下面是一个在 λ 不同时的图像

文中说 在λ=0.30时效果比较好
指数形式转化的特征：
1. 如果yt≤0, 不能进行指数转换，除非加一个常数，使其大于0
2. 转变通常对预测的作用不大，单会对预测区间有较大的影响

2.3.2 日期调整

例如，每月的牛奶需求，因为每个月天数不一样，预测精度可能会降低，如果改为每天的牛奶需求，预测结果会有改善

2.3.3 人口转换

比如有时候用总人口数为单位不如平均人口数的更具有解释性，比如中国人多钱多，但平均每人的前就不多了。

2.3.4 膨胀转换

在预测关于金融的事情的时候，由于货币膨胀率的不同，同样的数据可能会有不一样的意义。通常的做法是做如下转换

ynew−t=yt∗cpibasecpit

cpi 是Consumer Price Index消费者物价指数

2.4 预测精度评估

2.4.1 评估模型

yi^ 表示预测值 yi 表示观测值，设 ei=yi−yi^
则主要的评价指标有
1. 平均绝对误差MAE
2. 均方根误差RMSE

前两者仅用于比较数据规模相同的预测模型，后面可用于比较规模不同的模型
3. 平均绝对百分比误差MAPE，设 pi=100∗ei/yi

Mean absolute percentage error: MAPE=mean(|pi|).

这里可以看出，如果y趋向于0就会有接近无穷大的数值，显然不合理，而且它对于负值的惩罚比对正值更大
4. 均衡平均绝对百分比误差sMAPE

sMAPE=mean(200|yi−y^i|/(yi+y^i))

这种方法不好，就不在详细说了
5. 平均绝对比例误差 MASE mean absolute scaled error

qj=ej1T−1∑t=2T|yt−yt−1|.

对于周期不为1的比如季节性数据可用下式

qj=ej1T−m∑t=m+1T|yt−yt−m|.

对于普通数据

qj=ej1N∑i=1N|yi−y¯|.

整个误差公式为

MASE=mean(|qj|).

验证方法

要注意过拟的现象，所以要有测试集和交叉验证
测试集一般的比例为20%
交叉验证，时间序列交叉验证的方法为
1. 首先假设 K 个数值可以足够做好一个模型
2. 用 K+i 个做为验证，前 K+i−1 个作为训练集
3. 用前面的模型来评价准确率
4. 以上是用一个来计算的，大家可用类似的用一个特定的周期作为评价

2.5 残差诊断

残差检验模型

残差指的是 ei=yi−yi^ ，它有以下特性
1. 残差是不相关的
2. 残差的均值为0
3. 残差的方差为常数
4. 残差满足正态分布
后两者有时候可能不满足，但是如果前两者也不满足，可以用过调整改进算法，优化模型。但是不能完全依靠前两者评价模型的好坏。

自相关合成检验

ACF自相关检验只是看某一个的自相关，事实上如果进行很多次试验，如果有一个的ACF显示自相关程度很高，并不能充分的说明有自相关性，所以这里讲多个滞后期的ACF联合来看
Portmanteau tests for autocorrelation
主要讲了两种方法
1. Box-Pierce 方法

Q=T∑k=1hr2k,

h是最大滞后期数 （lag）但是不宜取太大，如果是没有季节性的建议取10，季节性的取2*季节周期m，另外如果这样取的h大于T/5,(T指样本数)，那么就取T/5
2. Ljung-Box

Q∗=T(T+2)∑k=1h(T−k)−1r2k.

这两种方法如何评价自相关性呢，
Q和Q*都满足自由度为（h-k）的 χ2 分布，k是参数的数量，于对源数据k=0 naive model没有参数，也取0

2.6 预测区间

通常我们预测的数值并不是一个单独的数值，而是一个区间，在置信度95%的区间中，预测值为

y^t±1.96σ^

σ^ 为预测值的标准差，通常时候如果模型中没有参数它等于残差的标准差，如果有参数，预测标准差会偏大些，但不会大太多

• 预测区间一般会随着预测时间的增长而增大，但是有些非线性方法并不会这样
  拓展阅读
  Maindonald, J. and H. Braun (2010). Data analysis and graphics using R: an example-based approach. 3rd ed. Cambridge, UK: Cambridge University Press.