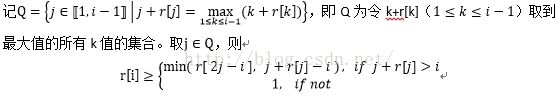[置顶] 练习：最长回文子串（Manacher算法）

【例题】

点击这里

【思路】

最长回文子串是个非常经典的问题，Manacher算法是解决它的O(n)优秀算法。

该算法提出在字符串相邻字符间插入字符，从而在中心拓展时无需考虑串长度的奇偶性（显然，对于任意长度为n的串，有n-1个间隔，故而补全串长度为2n-1，总为奇数）。

举个例子：原串str为abababa，长度为7。则补全串s为$#a#b#a#b#a#b#a#*，长度为17。其中#、$和*不属于原串字符集合，#为插入字符，$和*用来标记补全串边界，这方便了中心拓展比较，同时避免索引溢出。

设数组r，r[i]表示补全串s中，以字符s[i]为中心的回文串半径长度（半径含中心字符s[i]）。

一旦得出数组r，则只需遍历r并将ans置为最大的r[i]值，输出ans-1即为原串中回文串的最大长度。

可以证明，经过上面的补全后，对于任意i，补全串中以s[i]为中心的回文串去掉所有#后，长度为r[i]-1，即对应的原串中回文子串的长度。

如何求出数组r呢？显然在求r[i]时，要充分利用r[1]、r[2]……r[i-1]这些已经求出的信息。先在这里写出数学表达。

由集合Q确定r[i]的最小值后，还需尝试性地增大r[i]向外围扩展比较，直到遇见s[i-r[i]]≠s[i+r[i]]，则已找到以s[i]为中心的最长回文串。

上面的数学表述虽然严谨，但不够具象，下面对该数学形式作通俗阐述。

事实上，j+r[j]反映了1,2……i-1中已经找到的所有回文串的最大覆盖范围。如果j+r[j]<i，则前面的结果对求r[i]并没有作用，我们只能暂时置r[i]=1（一个字符本身，也是一个回文串），然后再向外拓展比较。否则，i则在前面的覆盖范围内，那么首先找到s[i]关于s[j]的对称字符s[j*2-i]，则s[i]、s[j*2-i]距以s[j]为中心的回文串边缘的长度均为j+r[j]-i，根据回文串的对称性可得，若r[j*2-i]< j+r[j]-i（以s[j*2-i]为中心的回文串是以s[j]为中心的回文串的子串），则在覆盖范围内可以确定r[i]=r[j*2-i] ; 若r[j*2-i]> j+r[j]-i，则以s[i]为中心的回文串可一直拓展至覆盖边缘。覆盖范围外的部分，则需要我们尝试增大r[i]，继续老老实实地比较。

更形象的表述，则可见下图（绿色为重叠部分，蓝色为s[j]中心串，黄色为s[j*2-i]中心串突出部分）：

【代码】

#include <stdio.h>
#include <string.h>
#define maxSize 1000010
#define min(x,y) (x<y)? x:y

long int manacher(const char *str)
{
    long int i,len=strlen(str);
    char s[maxSize*2+3];
    s[0]='$'; s[len*2+1]='#'; s[len*2+2]='*';
    for (i=0;i<len;i++) {s[2*i+1]='#'; s[2*i+2]=str[i];}

    long int r[maxSize*2+3], j=1; r[1]=1;
    for (i=2;i<=len*2;i++)
    {
        if (r[j]+j>i) r[i]=min(r[j]+j-i, r[2*j-i]); else r[i]=1;
        while (s[i-r[i]]==s[i+r[i]]) r[i]++;
        if (i+r[i]>j+r[j]) j=i;
    }

    long int ans=0;
    for (i=1;i<=len*2;i++) if (r[i]>ans) ans=r[i];
    return ans-1;
}

int main()
{
    char str[maxSize];
    int n,i;
    scanf("%d",&n);
    for (i=0;i<n;i++){scanf("%s",str); printf("%d\n",manacher(str));}
    return 0;
}