SAR成像基础知识急救箱（二）关于离散傅里叶变换

1 离散傅里叶变换

font face=”Times New Roman” color=black size=4>
不加证明的给出以下结论：

• 连续周期函数的傅里叶变换对应离散频谱；
• 连续非周期函数的傅里叶变换对应连续频谱；
• 离散（可以认为是上一种情况采样后的结果）非周期函数的傅里叶变换对应连续频谱（这个听起来很不可思议，但是都是公式推出来的结果，这种情况有一个专门的名字，叫离散时间傅里叶变换，DTFT）；
• 离散周期函数的傅里叶变换对应离散周期频谱。

以上都可以用公式进行推导，此处省去。有个规则可以帮助我们理解上面的结论：时域的离散（采样）对应频域的重复；时域的重复（周期）对应频域的离散。且一个域的周期对应对应另一个域的采样间隔。
现在并没有涉及到离散傅里叶变换（DFT），它是在上面提到的第四种情况的基础上稍微扩展得到的。因为实际中遇到的信号是有限长度，并不会是周期的，但是呢，我们可以把它看成是某一个周期函数的一个周期，然后，我们也在频域中找到一个周期。离散傅里叶变换就是用来描述这一有限长度时域信号和同等长度的频域信号的对应关系的。
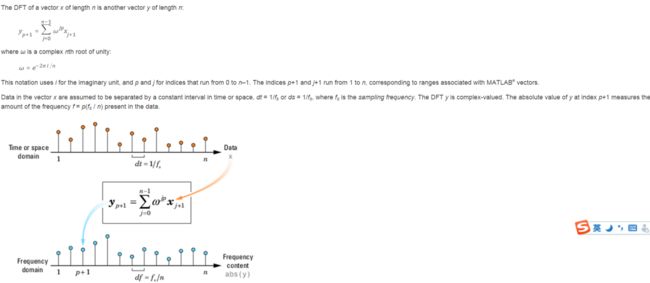
这个正变换及其对应的图形表示如下：

离散傅里叶正变换及示意图 （来源matlab）

注意图中一个域中的间隔和另一个域中的长度范围的对应关系。
离散傅里叶变换的意义是什么呢？可以说意义非常巨大，因为提出离散傅里叶变换之前，这个变换只是在理论上有意义，实际应用并不怎么样，因为现实中我们要处理的信号都是离散的且有限长度。
一般用快速傅里叶变换进行离散傅里叶变换。

2 补零

由于离散信号的离散时间傅里叶变以 2π  为周期，对一个周期取N个频率样本即为对应的离散傅里叶变换，因此利用DFT计算的 离散频谱的分辨率，即样本之间的间隔，为：

ΔΩ=2πN  

注意上面的间隔的单位为弧度（对应相位），不是弧度每秒。上式说明样本数决定了频谱的分辨率。反之亦然，频谱要求的分辨率决定了样本数。
时域的补零对应频域频谱变密；频域的补零对应时域的样本变密。注意根据上面图中的关系，如果一个域中的间隔不变，另一个域中的范围就不变。
下面的代码可以说明这一点：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
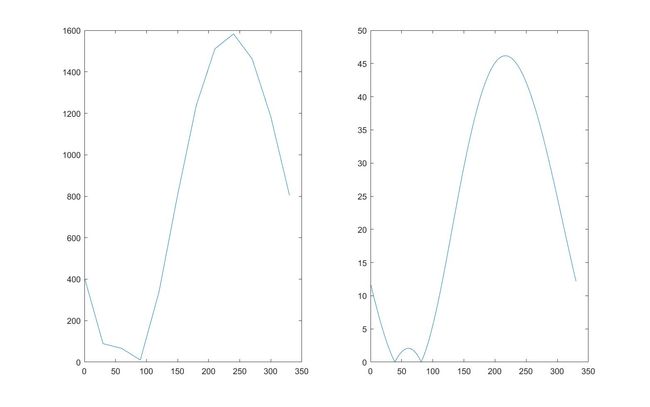
%这个说明了频域的补零对应时域的插值 

asc = 0:30:330; 
dec = [408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];

d = fftshift(fft(fftshift(dec.'))).';
d = [d,zeros(1,400)];           %补零
d = fftshift(ifft(fftshift(d.'))).';

subplot(1,2,1)
plot(asc,abs(dec))

subplot(1,2,2)
a = linspace(0,330,412); %注意既然频域的间隔没有变 那么时域的范围也就没有变化
plot(a,abs(d))

执行结果为：

3 离散傅里叶变换的两个应用

近似计算傅里叶变换步骤：
1、针对特定需求确定DFT所需的分辨率：

ΔΩ=ΔωT=2πN  

2、确定抽样时间间隔T：

Δω s =2πT >2Δω M  

其中 ω M   为连续时间信号的最高频率分量。（现在我有一个疑问：对于某一个我不知道规律的信号，我还没有进行傅里叶变换，我怎么知道最高频率分量，我怎么确定采样间隔，我怎么进行DFT？）
3、然后在NT秒的时间段内采集连续时间信号的N个样本。（这里N可能会根据不同的算法略有不同）。
4、计算DFT。
执行完以上步骤所得到的DFT的结果应是连续时间信号傅里叶变换的良好近似。

下面的代码实现了矩形脉冲信号的傅里叶变换：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
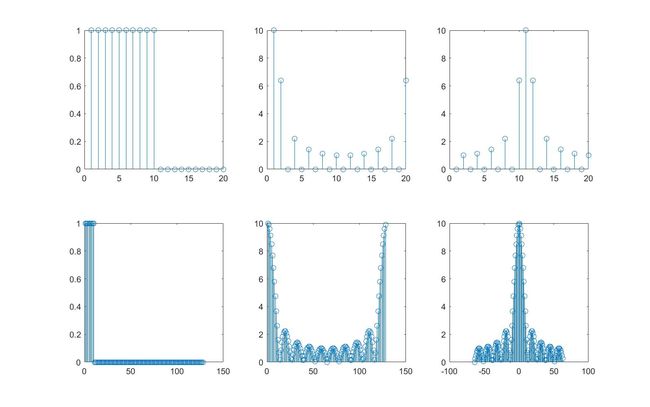
%一方面说明了利用DFT近似计算傅里叶变换
%另一方面说明了时域的补零对应了频域的内插 虽然频域的样本数增多了但是样本间隔缩小了，整体的频率范围没有变
T2 = [0:0.1:1.9]; 
%我们知道矩形脉冲的频谱是sinc函数，这个采样间隔是第一个零值点频率的10倍

xs = rectpuls(T2-0.5);
subplot(2,3,1);
stem(xs);

Xs = fft(xs);
subplot(2,3,2);
stem(abs(Xs));
Xks = fftshift(Xs);
subplot(2,3,3);
stem(abs(Xks));

m = zeros(1,108);
xs = [xs,m];%快速傅里叶变换前进行补零 也可以不补零
subplot(2,3,4);
stem(xs);

Xs = fft(xs,128);
subplot(2,3,5);
stem(abs(Xs));
Xks = fftshift(Xs);
np = [-64:63];
subplot(2,3,6);
stem(np, abs(Xks));

执行结果为：

利用离散傅里叶变换计算线性卷积
另外可以利用离散傅里叶变换计算线性卷积，前提是需要对两个序列（长度分别为N1和N2）分别补零至N1+N2-1。（为什么匹配滤波的时候没有
补零呢？因为那是循环卷积，这是两种不同的的运算。）