网络流算法详解
网络流算法在许多实际问题中有应用,如匹配问题,著名的Hall婚姻定理。这里不证明“最大流最小割定理”,简单解释求最大流的Ford-Fulkerson算法。接下来分别详述时间复杂度为O(VE2)的Edmonds-Karp算法和时间复杂度为O(V2E)的Dinic算法。至于较新的预留推进算法就不介绍了,这个算法证明比较难,感兴趣的可以看看算法导论。
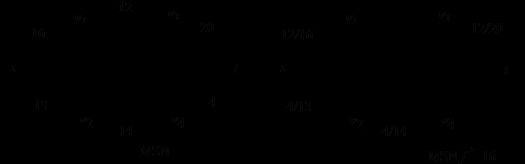
本文所用到的网络流如图1,s为原点,t为汇点,边上的值表示边的容量c(u,v),如c(s,v1)=15,c(v1,v2)=8。流用符号f(u,v)表示,如图2,流的容量f(s,v1)=10,f(v1,v2)=5。剩余容量cf(u,v)=c(u,v)-f(u,v)。在原剩余网络中找到一条流后,修改原网络边的剩余容量得到剩余网络Gf,如图3所示。注意剩余网络中有一些新添加的边即反向边的容量,为流的反馈。在图3中,有f(v1,v3)=5,那么有f(v3,v1)=-f(v1,v3)=-5,然后cf(v3,v1)=c(v3,v1)-f(v3,v1)=0-(-5)=5。
图1 网络流的一个例子
1.Ford-Fulkerson算法
算法的主要思想:
1)初始化一条容量为0的流f和一个剩余网络Gf,第一个剩余网络为原图G,每条边的剩余容量初始化为每条边的初始容量cf(u,v)=c(u,v)。
2)在剩余网络Gf中寻找增广路径p,取增广路径p中的边的剩余容量cf(u,v)最小值作为流的增量△f,使得f’=f+△f。修改剩余图中每条边的容量cf’(u,v)=cf(u,v)- △f得到剩余网络Gf。(补充说明:原算法中的△f可以为单位1)
3)重复步骤2),直到找不到一条增广路径为止。
寻找一条增广路径的方法如图4所示,然后确定增广路径上的流增量△f。本例中△f=3。
整个网络可以用邻接表或矩阵表示,网络的边即为矩阵中的元素,网络的节点则为矩阵一维的下标。这里网络中每条边最好用一个结构体表示。结构体包含边的容量和每次通过的流量这两个变量。
下面是一个例子:
Ford-Fulkerson算法的伪代码如下:
Ford-Fulkerson(G, s, t)
1 for eachedge (u, v) Î E[G] //初始化每条边的流量为0
2 { f[u, v]¬ 0
3 f[v, u]¬ 0
4 }
5 //Gf ¬ G //初始化剩余网络Gf为原网络G,这里不需要代码
6 while thereexists a path p froms totin the network Gf //网络中还存在增广路径,仍然进行迭代
7 {search a pathp from network Gf //Karp算法采用广度优先,Dinic算法采用深度优先
8 cf (p) ¬ Min{ cf (u,v) | (u, v) is inp} //确定增广路径上的流增量△f(p)= cf (p)
9 for eachedge (u, v) inp
10 { f[u, v]¬ f[u,v] +cf (p) //增加剩余网络中增广路径上每条边的流量
11 f[v, u]¬ - f[u,v] //显然该路径上反方向上的容量为负
12 cf [u, v] ¬ c[u,v] –f[u, v] //计算剩余网络Gf中的每条边的容量
13 cf [v, u] ¬ c[v,u] –f[v, u]
14 }
15 }
2. Edmonds-Karp算法
Edmonds-Karp算法与Ford-Fulkerson算法的区别在于在Ford-Fulkerson算法的第7行,Edmonds-Karp算法采用广度优先算法(BFS)寻找一条从s到t最短增广路径p代替Ford-Fulkerson的随机寻找一条从s到t增广路径p。
引理1:在网络G=<V,E>中,原点为s,汇点为t。Edmonds-Karp算法中,对于任意顶点v ÎV – {s,t},在剩余网络Gf中的距离df(s,v)和 df (v,t)随着流的增加而单调递增。(每次增加两个单位,这里要用到BFS生成最短路径的性质,由于这次的增广路径在剩余网络中已经是最短路径了,在新的剩余网络中,通过(s, v)的最短路径要增加。证明略)
引理2:流增加的总次数不超过O(VE)。
证明(1):若在剩余图Gf中的边(u, v)满足c(u,v)=cf(u, v),边(u, v)是一条关键边。每次进行增广路径扩充后,关键边(u, v)不会在该次的剩余网络Gf中出现。每次扩充至少会有一条关键边。可以证明网络中的每条边称为关键边至多|V|/2-1次。所以流增加的总次数为O(VE)。
证明(2):当边(u, v)在上一次剩余网络Gf中第一次称为关键边时,有df (s, v)= df (s, u) + 1成立。然后边(u, v)将不会在该次剩余网络Gf’中,边(u, v)下一次出现在某个剩余网络中的时候有,肯定有流通过边(v, u)。假设当这种情况发生时,有网络Gf’’的流为f’,我们有:
其中由引理1: df ‘ (s, v)³df (s,v),有
df’ (s,u)=df ‘ (s,v)+1³df (s,v)+1=df (s,u)+2
所以从s到u的路径中,当其中的一条边称两次为关键边的时候,s到u的距离增加2个单位。s到v的距离最长为n-1,那么s到u的最长距离为n-2。所以边(u, v)能成为关键边的次数最多为n/2-1次。所以流增加的总次数为O(VE)。
Edmonds-Karp算法的时间复杂度:O(VE2)
由引理2可知,流增加的总次数不超过O(VE),又每次扩充增广路径的时间复杂度为O(E),故Edmonds-Karp算法的时间复杂度为O(VE2)。
3.Dinic算法
Dinic算法要用到层次图的数据结构,即MSN(Multi-Stage Network)。MSN可由每次计算得到的剩余网络Gf再计算得到。
定义1:k-阶图,k-stage图(或网络)G = (V, E)是一个有向图,G的顶点集合被分成(k+1)³ 2个不相交的集合Vi,0£i £k。如果有边(u, v)∈E,则有uÎ Vi和v Î Vi+1,对某个i∈[0,k-1]成立。V0=s,Vk=t。k-阶图和k-阶图中的一条阻塞流如下图所示。图中6产生了一条阻塞流表示在该图上从原点s到汇点t再不可能增加新的流了。
定义2:饱和边,如果边(u, v)满足f(u, v)=c(u, v)。
定义3:流f 称为网络G的阻塞流,当且仅当从s到t的任何一条路径中都包含一条饱和边。
图6 k-阶图
Dinic算法中用到的MSN数据结构(多阶网络)如下图8所示。MSN可以在剩余网络Gf中用BFS算法构建,时间复杂度为O(|V|+|E|)。要得到Dinic算法使用的MSN还需要一些简答的处理,如图7中,利用BFS得到的MSN可能含有边不能到汇点t,所以在计算MSN的过程中需要将这种边除去。如图8中的边(v3, x)。
图7 一个剩余网络Gf
图8 剩余网络图7Gf的一个MSN
引理1:Dinic算法中每次迭代后,MSN的阶数至少增加2。
假设流f * 是一个由Gf计算得到的MSNf的阻塞流,f’=f+f*,令MSNf’和MSNf 为Gf’和Gf计算得到的MSN。df’ (s, t)和df (s, t)分别是在MSNf’和MSNf 上从s到t的最短路径。我们仅仅需要证明df’ (s, t)=df (s, t)+2,除非t不在MSN中。考虑任何一条从s到t 的路径p,明显有|p|=df’ (s, t)。如果我们假定路径p上所有的边都在MSNf’上,那么流f*将不是一条阻塞流,因为我们可以继续增大在MSNf上的路径p的流f的容量,使得MSNf上的路径p的边至少有一条边成为饱和边,那么该边将不会在MSNf’上出现。所以这里必有一条边(u, v)将不会在MSNf’上出现。令边(u, v)是在MSNf上出现而不会在MSNf’上出现的边。当边(u, v)再次出现的情况是因为边(v, u)成为增广路径p’上的一条饱和边。这意味着有df (s, v)=df (s, u)+1;df’ (s, u)=df’(s, v)+1。因为边(u, v)在路径p上,由第2节中的引理1可知,df(s, u) £df’ (s, u)和df(s, v) £df’ (s, v)成立。所以我们得到
df (s, t)= df (s, v)+ df(v,t)
= df (s, u) +1+df (v,t)
=( df (s, v)-1)+1+(df (u,t)-1)
=df (s, v)+1+df (u,t)-2
£df’ (s, v)+1+df’ (u, t)-2
=df’ (s, v)+df’ (u, t)-1
=df’ (s, v)+( df’ (v, t)-1)-1
=df’ (s, t)-2
引理2:Dinic算法迭代的轮数至多为,即计算MSN的次数为O(V)。
第一个MSN的计算式从流f初始化为0开始的(见后面算法伪代码),用Dinic算法又计算了MSN k次。由引理1可知,1+2k≦n-1,因为任何路径的长度,包括df (s, t)都小于或等于n-1,所以k £ ën/2û - 1,引理得证。
引理3:Dinic算法每次计算阻塞流的时间复杂度为O(VE)。
阻塞流的寻找可以采用DFS算法。在MSN中从源点s出发寻找一条阻塞流f *,初始化f *=0。我们利用栈Stack来构建DFS算法寻找一条阻塞流,压栈到最深的一个节点后,然后当一个节点v从栈Stack中Pop出来后,分两种情况讨论:
1)v=t
因为存储在栈Stack中的顶点序列从栈底到栈顶为一条从s到t的路径,也是MSN中从s到t的一条最短路径p。令cf(p)为路径p的容量。在剩余网路Gf中增加路径p上的流f*的容量至cf(p),然后计算新的MSNf’。对于在MSNf中的路径p的每条边(u, v),减去容量cf(p)。如果该边的容量减少至0后,就将该边标记成饱和边。在MSNf’中这条边就不存在了,相反在Gf’中会有一条反向的边出现。
2)v≠t
这意味着顶点v不能到达汇点t,也即是栈中的路径从s只能最终到达v不能到达t,需要退栈。从新选择新的边压栈。
每次DFS的时间为O(n),因为在MSNf中路径的长度最多为n-1,每次压栈到顶点t后,开始出栈,修改边的容量,若该边为饱和边则在MSNf中去掉该边。然后,继续退栈,寻找新的边入栈新的顶点,如此反复进行DFS收索直到一条阻塞流f*产生。实际情况中阻塞流f*产生后,MSNf中已经没有从源点s到达汇点t的边了。所以在MSNf中利用DFS寻找一条阻塞流f*的时间复杂度为O(VE)。
引理4:Dinic算法的时间复杂度为O(V2E)。
由引理2和引理3可知Dinic算法的时间复杂度为O(V2E)。
Dinic算法伪代码
Dinic (G, s, t)
1 for eachedge (u, v) Î E[G]
2 { f[u, v]¬ 0
3 f[v, u]¬ 0
4 }
5 Gf ¬ G
6 Compute the MSN for Gf starting from source s
7 while sink t is in MSN
8 { find a blocking flow f* in MSN
9 for eachedge (u, v) in G
10 { f[u, v]¬ f[u,v] +f*[u,v] }
11 ComputeGf for flow f
12 Re-compute MSNfor Gf
13 }
14 End
下面是Edmonds-Karp算法的一个例子
原网络
最后举一个Dinic算法的例子
原网络G,也是第一个剩余网络Gf
从上面的例子可以看出,Dinic算法迭代计算了2次,而Karp算法迭代计算了3次。
模板代码:
#include<cstdio>
#include<cstring>
#include<queue>
#include<cmath>
using namespace std;
const int Ni = 210;
const int MAX = 1<<26;
struct Edge
{
int u,v,c;
int next;
} edge[20*Ni];
int n,m;
int edn;//边数
int p[Ni];//父亲
int d[Ni];
int sp,tp;//原点,汇点
void addedge(int u,int v,int c)
{
edge[edn].u=u;
edge[edn].v=v;
edge[edn].c=c;
edge[edn].next=p[u];
p[u]=edn++;
edge[edn].u=v;
edge[edn].v=u;
edge[edn].c=0;
edge[edn].next=p[v];
p[v]=edn++;
}
int bfs()
{
queue <int> q;
memset(d,-1,sizeof(d));
d[sp]=0;
q.push(sp);
while(!q.empty())
{
int cur=q.front();
q.pop();
for(int i=p[cur]; i!=-1; i=edge[i].next)
{
int u=edge[i].v;
if(d[u]==-1 && edge[i].c>0)
{
d[u]=d[cur]+1;
q.push(u);
}
}
}
return d[tp] != -1;
}
int dfs(int a,int b)
{
int r=0;
if(a==tp)return b;
for(int i=p[a]; i!=-1 && r<b; i=edge[i].next)
{
int u=edge[i].v;
if(edge[i].c>0 && d[u]==d[a]+1)
{
int x=min(edge[i].c,b-r);
x=dfs(u,x);
r+=x;
edge[i].c-=x;
edge[i^1].c+=x;
}
}
if(!r)d[a]=-2;
return r;
}
int dinic(int sp,int tp)
{
int total=0,t;
while(bfs())
{
while(t=dfs(sp,MAX))
total+=t;
}
return total;
}
int main()
{
int i,u,v,c;
while(~scanf("%d%d",&m,&n)) //m为输入的边数,n为顶点数
{
edn=0;//初始化
memset(p,-1,sizeof(p));
sp=1;
tp=n;
for(i=0; i<m; i++)
{
scanf("%d%d%d",&u,&v,&c);
addedge(u,v,c);
}
printf("%d\n",dinic(sp,tp));
}
return 0;
}