查找——二叉排列树
/* *Copyright (c) 2015 , 烟台大学计算机学院 *All right resvered . *文件名称:二叉排列树.cpp *作 者: 郑兆涵 *查找——二叉排列树 */
编写二叉排列树,并运行,分析代码
编程代码:
//编写函数.并进行相关测试
#include <stdio.h>
#include <malloc.h>
typedef int KeyType;
typedef char InfoType[10];
typedef struct node //记录类型
{
KeyType key; //关键字项
InfoType data; //其他数据域
struct node *lchild,*rchild; //左右孩子指针
} BSTNode;
//在p所指向的二叉排序树中,插入值为k的节点
int InsertBST(BSTNode *&p,KeyType k)
{
if (p==NULL) //原树为空, 新插入的记录为根结点
{
p=(BSTNode *)malloc(sizeof(BSTNode));
p->key=k;
p->lchild=p->rchild=NULL;
return 1;
}
else if (k==p->key) //树中存在相同关键字的结点,返回0
return 0;
else if (k<p->key)
return InsertBST(p->lchild,k); //插入到*p的左子树中
else
return InsertBST(p->rchild,k); //插入到*p的右子树中
}
//由有n个元素的数组A,创建一个二叉排序树
BSTNode *CreateBST(KeyType A[],int n) //返回BST树根结点指针
{
BSTNode *bt=NULL; //初始时bt为空树
int i=0;
while (i<n)
{
InsertBST(bt,A[i]); //将关键字A[i]插入二叉排序树T中
i++;
}
return bt; //返回建立的二叉排序树的根指针
}
//输出一棵排序二叉树
void DispBST(BSTNode *bt)
{
if (bt!=NULL)
{
printf("%d",bt->key);
if (bt->lchild!=NULL || bt->rchild!=NULL)
{
printf("("); //有孩子结点时才输出(
DispBST(bt->lchild); //递归处理左子树
if (bt->rchild!=NULL) printf(","); //有右孩子结点时才输出,
DispBST(bt->rchild); //递归处理右子树
printf(")"); //有孩子结点时才输出)
}
}
}
//在bt指向的节点为根的排序二叉树中,查找值为k的节点。找不到返回NULL
BSTNode *SearchBST(BSTNode *bt,KeyType k)
{
if (bt==NULL || bt->key==k) //递归终结条件
return bt;
if (k<bt->key)
return SearchBST(bt->lchild,k); //在左子树中递归查找
else
return SearchBST(bt->rchild,k); //在右子树中递归查找
}
//二叉排序树中查找的非递归算法
BSTNode *SearchBST1(BSTNode *bt,KeyType k)
{
while (bt!=NULL)
{
if (k==bt->key)
return bt;
else if (k<bt->key)
bt=bt->lchild;
else
bt=bt->rchild;
}
return NULL;
}
void Delete1(BSTNode *p,BSTNode *&r) //当被删*p结点有左右子树时的删除过程
{
BSTNode *q;
if (r->rchild!=NULL)
Delete1(p,r->rchild); //递归找最右下结点
else //找到了最右下结点*r
{
p->key=r->key; //将*r的关键字值赋给*p
q=r;
r=r->lchild; //直接将其左子树的根结点放在被删结点的位置上
free(q); //释放原*r的空间
}
}
void Delete(BSTNode *&p) //从二叉排序树中删除*p结点
{
BSTNode *q;
if (p->rchild==NULL) //*p结点没有右子树的情况
{
q=p;
p=p->lchild; //直接将其右子树的根结点放在被删结点的位置上
free(q);
}
else if (p->lchild==NULL) //*p结点没有左子树的情况
{
q=p;
p=p->rchild; //将*p结点的右子树作为双亲结点的相应子树
free(q);
}
else Delete1(p,p->lchild); //*p结点既没有左子树又没有右子树的情况
}
int DeleteBST(BSTNode *&bt, KeyType k) //在bt中删除关键字为k的结点
{
if (bt==NULL)
return 0; //空树删除失败
else
{
if (k<bt->key)
return DeleteBST(bt->lchild,k); //递归在左子树中删除为k的结点
else if (k>bt->key)
return DeleteBST(bt->rchild,k); //递归在右子树中删除为k的结点
else
{
Delete(bt); //调用Delete(bt)函数删除*bt结点
return 1;
}
}
}
int main()
{
BSTNode *bt;
int n=12,x=46;
KeyType a[]= {25,18,46,2,53,39,32,4,74,67,60,11};
bt=CreateBST(a,n);
printf("BST:");
DispBST(bt);
printf("\n");
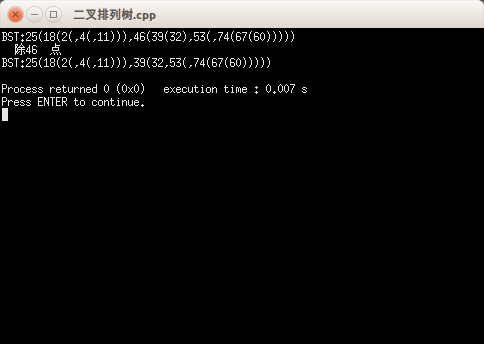
printf("删除%d结点\n",x);
if (SearchBST(bt,x)!=NULL)
{
DeleteBST(bt,x);
printf("BST:");
DispBST(bt);
printf("\n");
}
return 0;
}
输出结果:
以上代码为借鉴老师的代码,学生通过分析,并对下题进行结果测试:
问题:
认真阅读并验证二叉排序树相关算法:
(1)由整数序列{43,52,75,24,10,38,67,55,63,60}构造二叉排序树;
(2)输出用括号法表示的二叉排序树;
(3)用递归和非递归算法查找关键字55;
(4)分别删除43和55,输出删除后用括号法表示的二叉排序树.
编程代码:
以下代码分别为
(1)用递归方法查找,并删除关键字55:
//在bt指向的节点为根的排序二叉树中,查找值为k的节点。找不到返回NULL
BSTNode *SearchBST(BSTNode *bt,KeyType k)
{
if (bt==NULL || bt->key==k) //递归终结条件
return bt;
if (k<bt->key)
return SearchBST(bt->lchild,k); //在左子树中递归查找
else
return SearchBST(bt->rchild,k); //在右子树中递归查找
}
int main()
{
BSTNode *bt;
int n=10 ,x=55;
KeyType a[]= {43,52,75,24,10,38,67,55,63,60};
bt=CreateBST(a,n);
printf("BST:");
DispBST(bt);
printf("\n");
printf("删除%d结点\n",x);
if (SearchBST(bt,x)!=NULL)
{
DeleteBST(bt,x);
printf("BST:");
DispBST(bt);
printf("\n");
}
return 0;
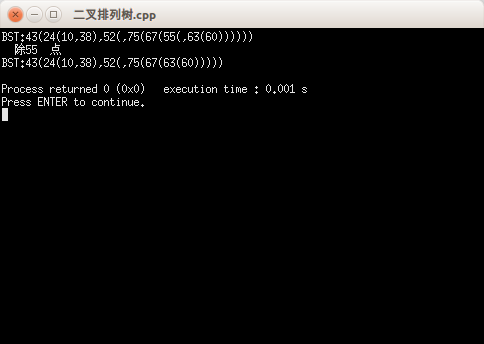
}输出结果:
(2)用非递归方法查找,并删除关键字43:
BSTNode *SearchBST(BSTNode *bt,KeyType k)
{
while (bt!=NULL)
{
if (k==bt->key)
return bt;
else if (k<bt->key)
bt=bt->lchild;
else
bt=bt->rchild;
}
return NULL;
}
int main()
{
BSTNode *bt;
int n=10 ,x=43;
KeyType a[]= {43,52,75,24,10,38,67,55,63,60};
bt=CreateBST(a,n);
printf("BST:");
DispBST(bt);
printf("\n");
printf("删除%d结点\n",x);
if (SearchBST(bt,x)!=NULL)
{
DeleteBST(bt,x);
printf("BST:");
DispBST(bt);
printf("\n");
}
return 0;
}
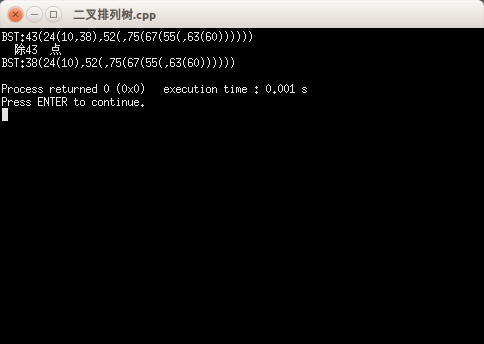
输出结果:
我的学习心得:
二叉排序树:
二叉排序树又称二叉查找(搜索)树,定义为:二叉排序树或者是空树,或者是满足如下性质的二叉树:
(1)若它的左子树非空,则左子树上所有元素的值均小于根元素的值;
(2)若它的右子树非空,则右子树上所有元素的值均大于根元素的值;
(3)左、右子树本身又各是一棵二叉排序树。
由二叉排序树(BST)性质可知,对于二叉排序树中任一元素x,其左(右)子树中任一元素y(若存在)的关键字必小(大)于x的关键字。如此定义的二叉排序树中,各元素关键字是唯一的。但实际应用中,不能保证被查找的数据集中各元素的关键字互不相同,所以可将二叉排序树定义中BST性质(1)里的“小于”改为“小于等于”,或将BST性质(2)里的“大于”改为“大于等于”,甚至可同时修改这两个性质。
从BST性质可推出二叉排序树的另外一个重要性质:中序遍历二叉排序树所得到的中序序列是一个递增有序序列。
typedef struct node //记录类型
{
KeyType key; //关键字项
InfoType data; //其他数据域
struct node *lchild,*rchild; //左右孩子指针
} BSTNode;首先定义结构体node类型是自定义类型typedef的,并且在其中定义关键字,以及关键字相关的信息data,再描述出左孩子和右孩子。
代码分析:
1.二叉排序树的插入和生成
在二叉排序树种插入一个新元素,要保证插入后仍满足BST性质。其插入过程时:若二叉排序树T为空,则创建一个key其域为k的节点,将它作为根节点;否则将k和根节点的关键字比较,若两者相等,则说明树种已有此关键字k,无须插入,直接返回0;若k<T->key,则将k插入到根节点的左子树中,否则将它插入到右子树中。对应的递归算法InsertBST()为:
//在p所指向的二叉排序树中,插入值为k的节点
int InsertBST(BSTNode *&p,KeyType k)
{
if (p==NULL) //原树为空, 新插入的记录为根结点
{
p=(BSTNode *)malloc(sizeof(BSTNode));
p->key=k;
p->lchild=p->rchild=NULL;
return 1;
}
else if (k==p->key) //树中存在相同关键字的结点,返回0
return 0;
else if (k<p->key)
return InsertBST(p->lchild,k); //插入到*p的左子树中
else
return InsertBST(p->rchild,k); //插入到*p的右子树中
}
此插入算法是在根节点指针为p(p可能为空)的二叉排序树种插入一个关键字值为k的节点,p的值可能发生变化,所以一定要用引用类型,即将p的值改变后的结果回传给实参,否则会出现错误。
二叉排序树的生成,是从一个空树开始,每插入一个关键字,就调用一次插入算法将它插入到当前已生成的二叉排序树中。从关键字数组A[0..n-1]生成二叉排序树的算法CreateBST()如下:
//由有n个元素的数组A,创建一个二叉排序树
BSTNode *CreateBST(KeyType A[],int n) //返回BST树根结点指针
{
BSTNode *bt=NULL; //初始时bt为空树
int i=0;
while (i<n)
{
InsertBST(bt,A[i]); //将关键字A[i]插入二叉排序树T中
i++;
}
return bt; //返回建立的二叉排序树的根指针
}
创建一个二排序树,其数据来源为,KeyType[]数组,n为n个数据。对于这个函数,首先需要将BSTNode*CreateBST进行初始化,此时树种没有节点,为空树。此时,通过while循环,利用InsertBST函数循环n次将A[i]这个数组插入到二叉排序树中。
每个节点插入时都需要从根节点开始比较,若比根节点的key值小,当前指针移到左子树,否则当前指针移到右子树,如此类推操作,知道当前指针为空,再创建一个节点,将当前指针指向它,这样便将这个节点插入到二叉排序树中了。因此可知,将任何节点插入到二叉排序树中,都是以叶子节点插入的。
对于一组关键字集合,若关键字序列不同,上述算法生成的二叉排序树可能不同。例如:关键字序列为{5,2,1,6,4,8,3,9}和关键字序列为{1,2,3,4,5,6,8,9},这两个关键字序列所生成的二叉排序树是不同的。
因为二叉排序树的中序序列是一个有序序列,所以对于任意一个关键字序列构造一棵二叉树,其实质是对此关键字序列进行排序,使其变为有序序列,“排序树”的名称也由此而来。通常将这种排序成为树排序,此排序的平均时间复杂度为O(nlog2n)。
2.二叉排序树上的查找
因为二叉排序树可看做是一个有序表,所以在二叉排序树上进行查找,和折半查找类似,也是一个逐步缩小查找范围的过程。递归查找算法SearchBST()如下:
//在bt指向的节点为根的排序二叉树中,查找值为k的节点。找不到返回NULL
BSTNode *SearchBST(BSTNode *bt,KeyType k)
{
if (bt==NULL || bt->key==k) //递归终结条件
return bt;
if (k<bt->key)
return SearchBST(bt->lchild,k); //在左子树中递归查找
else
return SearchBST(bt->rchild,k); //在右子树中递归查找
}
在bt指向的节点为根的排序二叉树中,查找值为k的节点。首先如果bt的值==NULL,或者bt->key==k,则说明无根后恰好能够找到所需要找到的节点,所以直接返回bt即可。如果不能够直接返回,需要观察查找的值是否小于根节点的值,如果小于,再通过递归在左子树中进行遍历查找,反之在右子树中进行递归的遍历查找。
非递归查找算法SearchBST()如下:
<pre name="code" class="cpp">BSTNode *SearchBST(BSTNode *bt,KeyType k)
{
while (bt!=NULL)
{
if (k==bt->key)
return bt;
else if (k<bt->key)
bt=bt->lchild;
else
bt=bt->rchild;
}
}
在bt指向的节点为根的排序二叉树中,查找值为k的节点。通过while循环,如果bt !==NULL,即bt不等于根节点,则直接返回bt,如果bt中的k值小于bt->key则将bt赋值为bt->lchild;反之则赋值为bt->rchild。
由上得出,在二叉排序树上进行查找,若查找成功,则是从根节点出发走了一条从根节点到查找节点的路径;若查找不成功,则是从根节点出发走了一条从根到某个叶子节点的路径。因此与折半查找类似,和关键字比较的次数不超过树的深度。