UFLDL 10 建立分类用深度学习网络

1 微调 Fine-tune

上节中，介绍了利用自编码器和未标注样本，通过自学习或者样本更加本质的特征，这一节将会使用已标注样本对其进行微调，提高分类精度。

以上是通过自学习获得的分类器，整个过程分为两部分：
1. 先通过自学习得到特征层（a1,a2,a3）
2. 使用分类器（图中可以看做是logistic）和得到的新特征进行分类
显然，我门的已标注样本仅仅在在第二部分起作用，而第一部分也是对于分类很重要的步骤，所以，这里的想法是使用已标注样本对第一部分的参数W1进行进一步的微调。
微调的方法是：
使用梯度下降或者其他方法调整W1,使样本误差进一步减小。
值得注意的是，如果使用上面介绍的微调的方法，那么使用“替代replacement”和使用“级联concatenation”效果相似，所以一般使用占用内存更小的代替的方法。

另外，上面微调的效果在拥有大量的已标注样本时会有较好的效果，但是如果只有少量已标注样本，那么微调的效果可能会非常有限。

2 深度网络概述

前面的分类器中最终进入分类器的特征值 ali ，只经过一层隐藏单元计算，这类神经网络分类器叫作浅层神经网络，如果中间多加几层就是所谓的深层网络。

2.1 深层网络的优势

为什么要使用深度网络呢？
在Yoshua Bengio的Learning Deep Architectures for AI中第二章有叙述。
主要原因是some functions cannot be efficiently represented by architectures that are too shallow.也就是说，深度网络比起浅网络更容易表达出我们需要的功能。
这里有一个例子：逻辑电路判断奇偶性，表达式如下

这里有一个定理，如果我们拥有一个仅仅由一个输入层、一个隐层以及一个输出层构成的网络，那么该奇偶校验函数所需要的节点数目与输入层的规模 n 呈指数关系。但是，如果我们构建一个更深点的网络，那么这个网络的规模就可做到仅仅是 n 的多项式函数。
另外还有个优点是，在多层网络中的部分节点可以被重复利用，如下图:

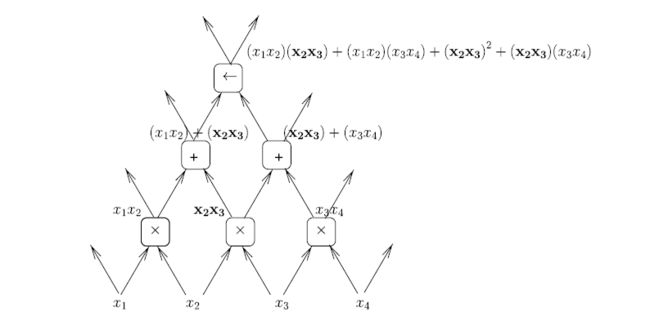
其中的x2x3被利用了多次。
是用于处理图像时，可以将各特征逐步组合得到更加复杂的特征。
我们大脑也是使用了深层网络，进行视觉工作时，在大脑皮层会有5-10层的深度。

2.2 深度神经网络的训练

2.2.1 为什么深度神经网络难以被训练？

http://neuralnetworksanddeeplearning.com/chap5.html
其翻译版
http://www.jianshu.com/p/917f71b06499?utm_source=tuicool&utm_medium=referral

首先引入一个栗子，手写识别问题。
在http://neuralnetworksanddeeplearning.com/chap5.html的试验中，利用bp算法，当使用一层神经网络时其准确率是96.48%，使用二层的结果是96.90%，使用三层的结果是 96.57%，使用四层的结果是96.53%。

我的天呢？上面说了这么多多层神经网络的好处，这里为什么会出现层数越多得到的训练结果越差呢？？
这里我们分析下一共四层神经网络时每一层模型的训练情况，下图为每一层的学习速度：

可以发现第一层的训练速度只有只有一层的1/100，（(⊙o⊙)…还是没有说出这意味着什么,），还记得我们设置神经网络时，初始设置是随机的不同值，也就是说第一层的初始值也是很乱，没有道理的，丢了大部分的原始信息的，如果出现这种情况（第一层训练速度非常慢），就会造成第一层在迭代了500次之后，还是没有很好的将原始数据的特征表达出来，即使后面的模拟再好，也无济于事！
下面一节就会介绍为什么会出现这种情况，大家可以根据自身需要选择性忽略，直接跳到下下节

2.2.2 梯度消失的原因

上面的情况就叫做梯度消失。
为何会出现这种情况呢？
为了说明这个问题，我们建立一个四层，每层一个节点的神经网络，其中的b1 b2…都是偏差:

其中 zj=wjaj−1+bj
这里我们设z是输入神经元的值，a是输出该神经元的值，当然也是输入下一个的神经元的值的一部分。
现在我们查看第一个神经元的梯度 ∂C∂b1 ,其公式如下

该公式对后面的理解至关重要。
该公式的解释如下：
假设b1的变化为Δb1. 那么他会引起其输出值的变化 Δa1，进而会引起第二个输入值的变化Δz2……………最终会引起损失函数C的变化 ΔC。设：

也就是说我们可以通过分析各项的变化值得到最后的表达式，我们从头开始分析：
a1=σ(z1)=σ(w1a0+b1) 所以考虑b1的变化对a1的影响：

Δa1≈=∂σ(w1a0+b1)∂b1Δb1σ′(z1)Δb1.

同理： z2=w2a1+b2

Δz2≈=∂z2∂a1Δa1w2Δa1.

整合一下：

Δz2≈σ′(z1)w2Δb1.

聪明的你一定知道下面是类似的分析下去，得到：

ΔC≈σ′(z1)w2σ′(z2)…σ′(z4)∂C∂a4Δb1.

两边同时除以 Δb1 就得到了下面的公式：

∂C∂b1=σ′(z1)w2σ′(z2)w3σ′(z3)w4σ′(z4)∂C∂a4.

明白了上面的公式的含义，让我们来探究为啥会有梯度消失呢？
分析一下上面的公式，其中很多 σ′ ，我们看一下他的图像：

可见其最大值为0.25，我的天呢，如果很多个相乘那么乘积就很小了，也就是说层数越多，得到的结果越小，我的天呢，这就是数学的神奇！

2.2.3 梯度爆炸

其实上面的推理还不太严谨，虽然一般情况下，w的值我们初始化时都将其设置为小于1的值，但是如果我们人为的将w的值设置为一个较大的值（大于1/0.25，比如100），那么上面的公式的乘积就会越来越大，而且成指数暴增，这就会造成梯度爆炸的情况。梯度太大也不会得到一个很好的结果，容易错过最佳值。

2.2.4 梯度不稳定问题

看了上面的问题和解释，你也许会说把w弄的适当大小不就行了么？其实如果增加w，经常会使 aw+b 变大更多，从 σ′ 的图像可以看出，此时的值非常小，所以非常可能出现梯度弥散，那么可以将其设置为接近1么？答案是可能，但是很难满足这样的条件。
其实上面不论是地图弥散还是梯度爆炸，其原因都是前面几层的梯度值来自于乘积的形式，这就会造成不稳定性的累积，各层很难都以相似的调整，所以计算方法不改，这种问题很难解决。

2.2.5 其他问题

尽管上面是按照只有一个节点的神经网络来推理的，但是有多个节点时结果也是类似的，而且会更加复杂，所以以上问题还是会出现；另外还会出现例如局部最小值等问题。

2.3 Greedy layer-wise training 逐层贪婪训练

由于上面的原因，我们没法使用一般的bp方法训练神经网络，但是以后将要介绍的 逐层贪婪训练 要更好一些。
这里先简单的说一下：逐层贪婪算法的主要思路是每次只训练网络中的一层，即我们首先训练一个只含一个隐藏层的网络，仅当这层网络训练结束之后才开始训练一个有两个隐藏层的网络，以此类推。在每一步中，我们把已经训练好的前 k-1 层固定，然后增加第k 层。每一层的训练可以是有监督的（例如，将每一步的分类误差作为目标函数），但更通常使用无监督方法（例如自动编码器，我们会在后边的章节中给出细节）。这些各层单独训练所得到的权重被用来初始化最终（或者说全部）的深度网络的权重，然后对整个网络进行“微调”（即把所有层放在一起来优化有标签训练集上的训练误差）.
上面可以看出，这种方法除了可以避免梯度不稳定的问题，也可以使用无监督学习，减少对标注样本的依赖。
另外使用无标签数据训练完之后得到的参数已经比较靠谱了，即使是局部解也是比较好的局部解了，再使用微调的方法得到的结果会更好。

3 Stacked Autoencoders 嵌入自编码

官方翻译成“栈式自编码算法”，感觉这个太高大上，不容易理解，其含义就是使用自编码器进行逐层的贪婪算法，训练每一层的参数时都使用自编码器：
即先利用原始输入来训练网络的第一层，得到其参数 W(1,1),W(1,2),b(1,1),b(1,2) ；然后网络第一层将原始输入转化成为由隐藏单元激活值组成的向量（假设该向量为A），接着把A作为第二层的输入，继续训练得到第二层的参数 W(2,1),W(2,2),b(2,1),b(2,2) ；最后，对后面的各层同样采用的策略，即将前层的输出作为下一层输入的方式依次训练。其中每次都会去掉输入输出，只留下稀疏编码部分作为隐含层。
应该比较好理解，这里就不在复述栗子了，需要的可以到官网拿。
另外：
如果网络的输入数据是图像，那么网络的第一层会学习如何去识别边，第二层一般会学习如何去组合边，从而构成轮廓、角等。更高层会学习如何去组合更形象且有意义的特征。例如，如果输入数据集包含人脸图像，更高层会学习如何识别或组合眼睛、鼻子、嘴等人脸器官。

4 微调

这里的微调也是用已标注样本对其原有数据进行反向传播调整参数，与第一小节的内容相似。

5 线性解码

使用自编码网络时，还会有一个问题：
其输出层为
这里的a3,因为是f的输出值，如果f是sigma函数，那么他的值应该在0-1范围内，但是我们的初衷是将输出值对输入值复现。
所以我们有时候需要先将输入值预先缩放到一定的空间中，这里我们有另外一种方法：线性解码器。
他的原理就是对最后输出层设立一个恒等函数（线性激励函数），讲输出值的空间进行缩放。
这里课设最后的线性激励函数为

适当设置w就可以使x的值的范围在0-1之外
这样设置还会影响 的问题是当利用反向传播时，其误差项会改变：

因为在输出层激励函数为 f(z) = z, 这样 f’(z) = 1
所以