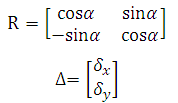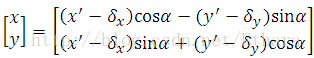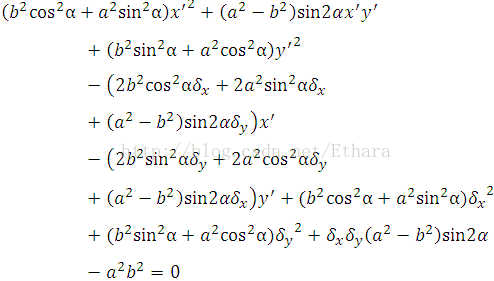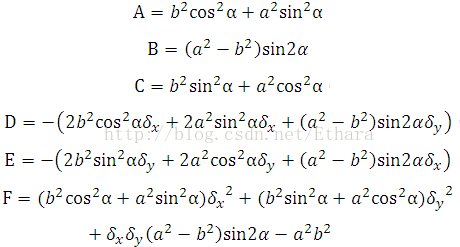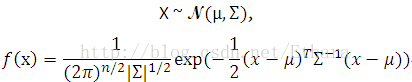Contour of Gaussian Distribution
Contour of Gaussian Distribution
Ethara
How much do you know about ellipse especially when I present you with an equation like this,
Chances are that you will fail to obtain an intuitive interpretation on its analytical shape in the 2-dimensional Cartesian coordinate.
As a matter of fact, (1) is the general form of an ellipse equation. An ellipse formalized by (1) can be obtained by linear transformation on the standard form (2). And matrix multiplication plays an essential role of this process.
Proof:
Suppose P = (x, y)T is the point conforming to (2), P' = (x',y')T is the corresponding point after a series of linear transformations including rotation and shift. Algebraically, rotation transformation is represented by matrix R parameterized by the rotation angle (anticlockwise), and shift transformation by matrix delta.
Using linear transformation, we have,
Solve for P,
After expansion, we obtain,
Further,
Plug it back to (2),
Finally, we obtain the following general form (*) that P’ conforms to analytically and explicitly,
Apparently, referring to (1),
Consequently, we are done with the proof.
Analysis:
The parameter B in (*) can be regarded as the proof to discriminate whether there exists a rotation in the linear transformation while D and E are to check the existence of a shift.
If a equals to b, equation (*) degenerates to
where the cross term is eliminated. This indicates that, no matter how the pattern is rotated, it stays the same, which only a circle in 2-dimensional plane can achieve.
More properties of (*) can be derived by choosing some particular values.
Those who noticed the topic must now be confused with the irrelevant discussion above. Let me head for the highlight, the elliptical contour of Gaussian distribution.
Given a continuous-valued random variable,
The above figure shows the standard normal distribution (2-dimensional) with mean zero and covariance matrix sigma = I(the 2 by 2 identity matrix).
More generally, to see the contour of the 2-dimensional Gaussian distribution, we make the following assumptions,
To solve for the contour of a Gaussian distribution, we have,
where z0 conforms to z = z0, parallel to the plane xoy and X = (x,y)T.
Further,
where
Referring to (*), we arrive at a conclusion that the contour of a Gaussian distribution is an axis-parallel ellipse exactly when
and is a circle when
The figure above shows an elliptical contour of a 2-dimensional Gaussian distribution with
On the other hand, the mean of a Gaussian distribution, mu, changes the position of the bell-shaped curve surface only.
Acknowledgement
This work has benefited greatly from the discussion with my comrade, C. Huang, who is a graduate-to-be of Peking University. Figures and data are from the handout of Andrew Ng's Coursera, Machine Learning.
Postscript
Inevitably, there might be some mistakes in the above discussion and derivation. I’m looking forward to your opinions and corrections. Thanks.