最小生成树算法(引自《算法导论》)
http://rock3.info/blog/2013/10/21/%E6%9C%80%E5%B0%8F%E7%94%9F%E6%88%90%E6%A0%91%E7%AE%97%E6%B3%95%EF%BC%88%E5%BC%95%E8%87%AA%E3%80%8A%E7%AE%97%E6%B3%95%E5%AF%BC%E8%AE%BA%E3%80%8B%EF%BC%89/
一、概念
找有权无向连通图(连通图本身就是无向图,强连通图指有向图所有节点都双向连通)的所有边的权重合最小的连通子图的过程,就是找最小生成树的过程。用数学语言描述这一过程:
一个无向连通图G=(V,E),其中V是顶点集合,E是边集,对于图G中的任意一条边(u,v)属于E,都有一个权值w(u,v)表示连接u和v的代价,我们希望找到一个无回路的子集T属于E,T连接了所有的顶点,且其权值之和w(T)最小。因为T包含所有定点,又没有回路,所以它必然是一棵树,成为生成树(spanning tree),因为它“生成”了图G。把确定树T的问题称为最小生成树问题。
IEEE的802.1标准中定义的STP,RSTP等协议都是最小生成树的具体应用。
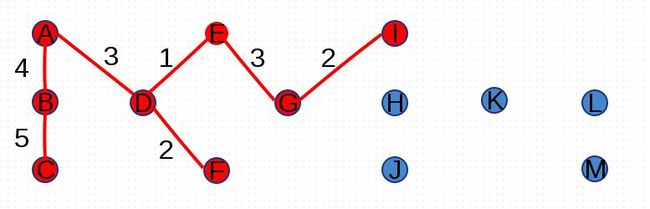
找最小生成树通常有两种算法,它们分别是Kruskal算法和Prim算法。其中Kruskal算法从边入手,Prim算法从点入手。本篇博客以下图为实验对象:
二、Kruskal算法
Kruskal,通常音译为“克鲁斯卡尔”,其算法的基本想法是不断增加权重最小的边、边上的两点,但并不形成回路,直至找到最小生成树。对于给定的无向有权图G=(V,E),Kruskal算法描述如下:
1、构造空集合A,并将图G中所有点加入集合A,此时A为有|V|棵树的森林。
2、将图G中所有边按照权重进行排序,形成有序集合B。
3、对于步骤2中排序后集合B中权重最小的边(u,v),尝试将(u,v)以及点u、v加入到集合A中。
4、如果步骤3中尝试加入的点和边,对于图A而言,不形成回路,则添加点u、v及边(u,v),否则不添加。
5、将步骤3处理的边(u,v)从集合B中删除。
6、判断此时作为图的集合A,是否满足边的数量等于|V|-1(也即满足最小生成树的要求),如果是,则找到最小生成树,如果不是,则转至步骤3。
下面结合本篇博客的例子,给出一个使用Kruskal算法找最小生成树的过程:
首先,构造一个空集合A,兵家图G中的所有点加入A中,此时A为由13棵树组成的森林:
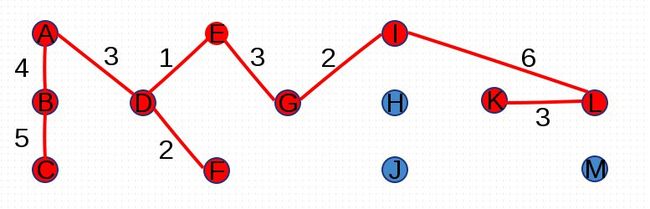
其次,将图G中的所有点按照权重排序:
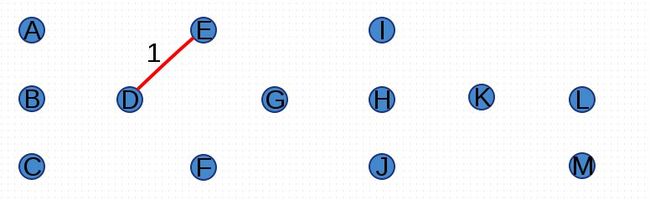
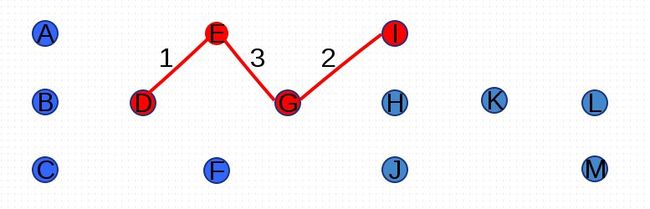
再次,进行反复尝试将图G中的边按照权重由小到大的次序添加到集合A中,并判断是否形成环路,尝试添加权重为1的边(D,E):
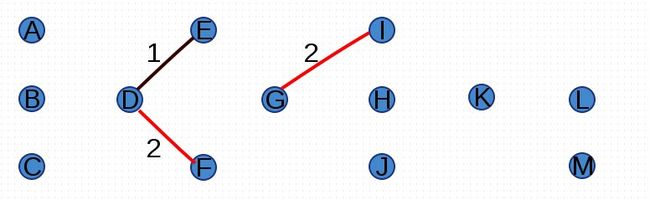
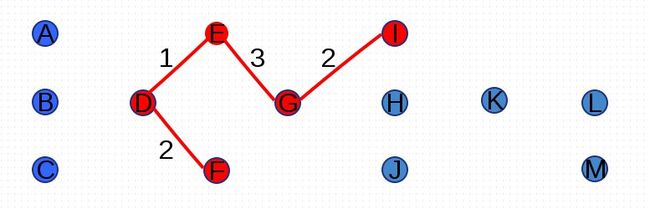
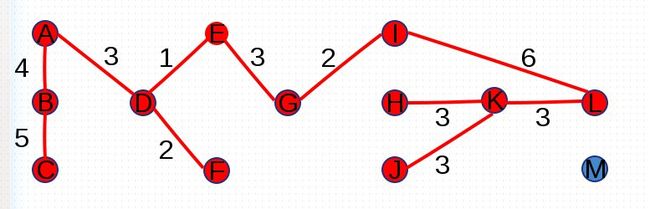
尝试添加权重为3的边(A,D)、(E,G)、(H,K)、(K,L)、(J,K): 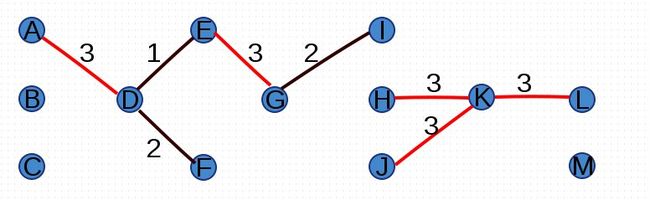
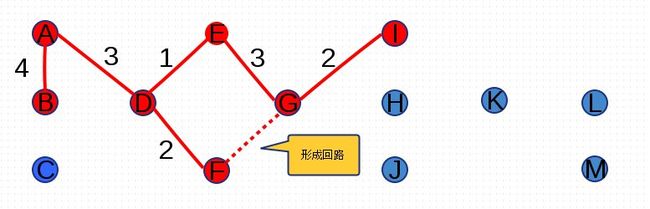
尝试添加权重为4的边(A,B)、(F,G),由于边(F,G)添加后形成环路,因此放弃添加(F,G): 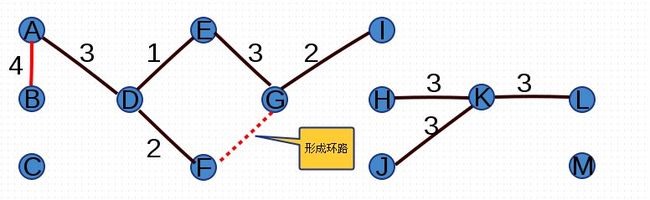
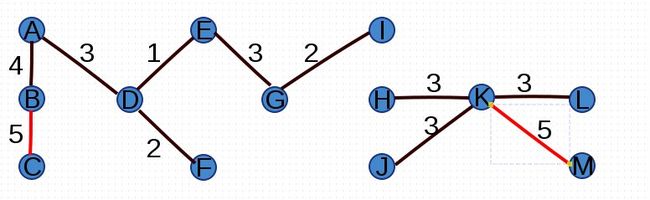
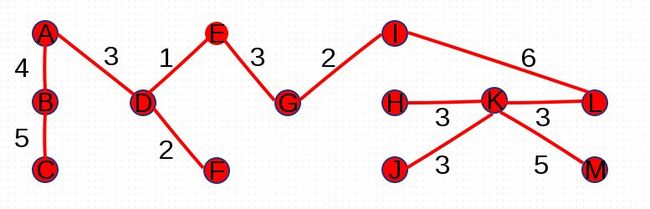
添加完(I,L)后,没有形成环路,并且所有顶点均连通,因此最小生成树找到: 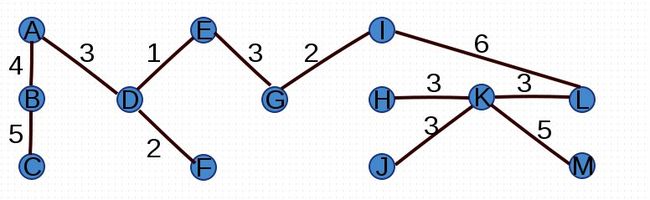
至此,最小生成树已经形成,所有边的权值合为1+2+2+3+3+3+3+3+4+5+5+6=40。
从上述方法不难看出,权重较小的边,尽量多的被保留到最小生成树中,而权重较大的边基本上被排除在最小生成树中,因此,我想(个人习惯),将Kruskal方法形象的叫做“增边法”,类似的,也可以采用“减边法”去找最小生成树,大体方法应该是将所有边按照降序排序,然后按照权重由大到小的方式在原图G中减去权值最大的边,判断原图是否连通。“减边法”同样属于Kruskal算法行列。
三、Prim算法
Prim算法,多翻译作“普里姆”,与Kruskal算法的想法基本差不多。不过Prim从点入手,而非从边入手。
Prim算法的基本像法是不断扩大点集合,并在以点集合中所有点相关的边中权值最小的且不构成回路的,不断加入集合,最终构成最小生成树。对于图G=(V,E),Prim算法描述如下:
1、给定空集合A,以及任何一点v0属于{V},将v0加入集合A中,此时A={v0}。
2、对于集合A中的任意一点u,以及V-A中任意一点w,找到权重最小的边(u,w),尝试将(u,w)加入集合A。
3、判断步骤2中的边(u,w)是否使图A形成回路,如果形成回路,则不加入A,否则将点w和边(u,w)加入A。
4、判断此时图G中所有点{V}是否已经全部加入到集合A中,如果是,则最小生成树已经找到,退出;否则,转步骤2。
下面结合本篇博客的例子,给出一个使用Prim算法找最小生成树的过程:
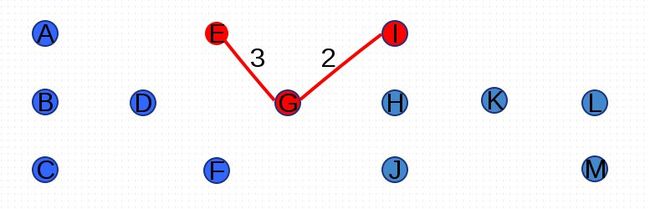
首先,任意选择图G中的一个顶点,在此我选择I顶点:
与顶点I相连接的权重最小的边是(G,I),权重是2,加入后经判断不形成回路,也没包含图G中所有顶点: 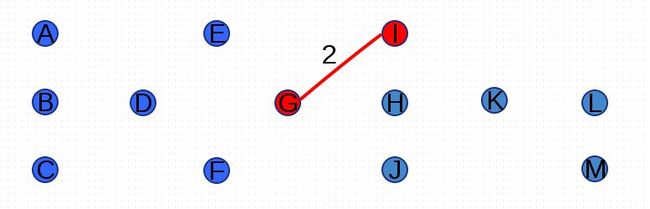
四、改进
Kruskal算法和Prim算法的时间复杂度均为O(ElogV),因为这两中算法都是用普通的二叉堆,如果采用斐波那契堆,Prim算法的时间复杂度可以减少到O(E+VlogV),如果|V|远小于|E|的话,这将是对该算法的较大改进。