hihocoder-1050 树中的最长路(dfs)
树中的最长路:http://hihocoder.com/problemset/problem/1050
- 样例输入
-
8 1 2 1 3 1 4 4 5 3 6 6 7 7 8
- 样例输出
-
6
描述
上回说到,小Ho得到了一棵二叉树玩具,这个玩具是由小球和木棍连接起来的,而在拆拼它的过程中,小Ho发现他不仅仅可以拼凑成一棵二叉树!还可以拼凑成一棵多叉树——好吧,其实就是更为平常的树而已。
但是不管怎么说,小Ho喜爱的玩具又升级换代了,于是他更加爱不释手(其实说起来小球和木棍有什么好玩的是吧= =)。小Ho手中的这棵玩具树现在由N个小球和N-1根木棍拼凑而成,这N个小球都被小Ho标上了不同的数字,并且这些数字都是出于1..N的范围之内,每根木棍都连接着两个不同的小球,并且保证任意两个小球间都不存在两条不同的路径可以互相到达。总而言之,是一个相当好玩的玩具啦!
但是小Hi瞧见小Ho这个样子,觉得他这样沉迷其中并不是一件好事,于是寻思着再找点问题让他来思考思考——不过以小Hi的水准,自然是手到擒来啦!
于是这天食过早饭后,小Hi便对着又拿着树玩具玩的不亦乐乎的小Ho道:“你说你天天玩这个东西,我就问你一个问题,看看你可否知道?”
“不好!”小Ho想都不想的拒绝了。
“那你就继续玩吧,一会回国的时候我不叫上你了~”小Hi严肃道。
“诶!别别别,你说你说,我听着呢。”一向习惯于开启跟随模式的小Ho忍不住了,马上喊道。
小Hi满意的点了点头,随即说道:“这才对嘛,我的问题很简单,就是——你这棵树中哪两个结点之间的距离最长?当然,这里的距离是指从一个结点走到另一个结点经过的木棍数。”。
“啊?”小Ho低头看了看手里的玩具树,困惑了。
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第一行为一个整数N,意义如前文所述。
每组测试数据的第2~N行,每行分别描述一根木棍,其中第i+1行为两个整数Ai,Bi,表示第i根木棍连接的两个小球的编号。
对于20%的数据,满足N<=10。
对于50%的数据,满足N<=10^3。
对于100%的数据,满足N<=10^5,1<=Ai<=N, 1<=Bi<=N
小Hi的Tip:那些用数组存储树边的记得要开两倍大小哦!
输出
对于每组测试数据,输出一个整数Ans,表示给出的这棵树中距离最远的两个结点之间相隔的距离。
法一:
利用树的性质:树上任意某个节点到树上任意节点的最远距离的端点一定会是树上某一个直径的两个端点之一
#include <cstdio>
#include <cstring>
using namespace std;
struct Node {
int e,nxt;
}node[200005];//数组模拟链表
int n,num,maxDep,nd;
int h[100005];
void add(int s,int e) {//加边
node[++num].e=e;
node[num].nxt=h[s];
h[s]=num;
}
void dfs(int dep,int u,int pre) {
if(dep>maxDep) {//如果该路径的长度大于maxDep,更新maxDep和最长路的端点
maxDep=dep;
nd=u;
}
int i=h[u];
while(i) {
if(node[i].e!=pre)//因为是树,所以只用判断当前节点的前一个节点是否与其下一个节点相同
dfs(dep+1,node[i].e,u);
i=node[i].nxt;
}
}
int main() {
int s,e,i;
while(1==scanf("%d",&n)) {
memset(h,0,sizeof(h));
num=0;
for(i=1;i<n;++i) {
scanf("%d%d",&s,&e);
add(s,e);
add(e,s);
}
maxDep=0,nd=0;
dfs(0,1,0);//找到最长路的一个端点
maxDep=0;
dfs(0,nd,0);//找到最长路的长度
printf("%d\n",maxDep);
}
return 0;
}
法二:
官方提示:路总有折点,路径也不例外!
小Ho为了能够回国也是很拼,但是一连思考了几天却仍然毫无结果,虽然仍然是在折腾自己的树玩具,但是却没有了那种单纯的快乐……小Ho无奈之下,只得乖乖去请教小Hi。
小Hi仿佛早就知道这个死脑筋不知道什么叫举一反三的同伴即将到来,马上递上了一张画着小Ho树玩具千千万万种形态中的一种。
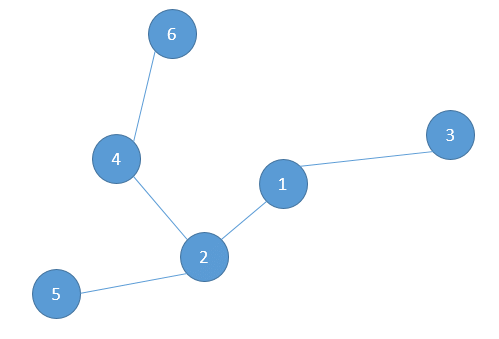
“你且看看这棵树。”小Hi道:“你可知道这棵树里的最长路是哪一条么?”
“唔……应该是6-4-2-1-3这一条吧,它的长度是4。”这个图的结点数并不多,小Ho一眼便看了出来。
“那好,那么接下来我们把你的这棵树画成更像树一点,比如——给它指定一个根节点(注意啦!这里的根节点的意义指的是整棵树的根节点,而后文中出现的一些根结点的意思是这棵有根树中某棵子树的根节点,并不是说将这棵树另外指定一个根节点并且重新绘制!!),不如就1号结点把~”小Hi愉快的又画了一张图,递给了小Ho。
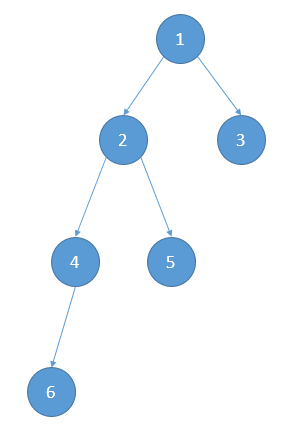
“好的……不过这,说明了什么?”小Ho摸不着头脑。
“你看这条最长路,是否在1号结点这里转折了一下?”小Hi问道。
“是啊,但是这不能说明什么吧?如果我以5号结点为整棵树的根节点重新绘制,那么这条最长路并不会在5号结点这里转折一下啊?”小Ho更加犯迷糊了。
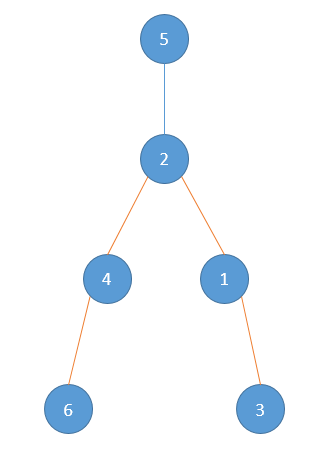
“不不不,我不是想说在根节点转折——最长路当然不会经过每一个根结点啦,不然那不就是经过每一个结点了。我想说的是转折点存在的这个事实!”
“但是,如果我以3号结点为整棵树的根结点的话,那么就没有转折吧!”小Ho发现了一个盲点。
“你以为你是华生啊!还盲点呢!这种情况下,肯定是因为3号结点有且仅有一个子结点——不然这就和最长路矛盾了,这种时候我们可以视作它还有一个子结点——也就是它本身,不过它到这个子结点的距离就是0而已~”小Hi努力的圆话。
“如果你要这么说的话……好吧,我承认这个转折点的存在,所以呢?”
“既然你接受了这个设定,那么想来应该就会发现——如果设最长路的转折点为t,以t为根结点的子树中深度最深的叶子结点为l,以t为根结点的子树中不与l在t的同一棵子树中且深度最深的叶子结点为l2,那么最长路的长度就等于以t为根结点的子树中l的深度与l2的深度之和!”小Hi解释道。
“等等……你说太快了,我没能理解!”小Ho跟不上节奏了。
“你看……这个图中,以1号结点为根结点的子树中最深的叶子节点是6号结点是吧。”

“没错,我还知道,这棵树中不与6号结点在一棵子树中而且深度最深的结点就是3号结点,的确这样算出来就会是最长路,但是有没有可能这只是一个特例呢?”小Ho反问道。
“好的,我来证明给你看吧,我们要找的答案其实就是2个点l'和l2',这两个结点便是最长路的两个端点是不是?”小Hi整理了下思路,说道。
“没错,我想想,你说的‘转折点’其实就是这两个结点的最近公共祖先对不对?”小Ho问道。
“反应很快嘛,那么如果我知道了这个转折点——不妨也就设为t,我该如何求l'和l2'呢?”小Hi继续问道。
“也就是说我要找到t这棵子树中的两个结点l'和l2',使得dist(t, l') + dist(t, l2')——dist(a, b)表示结点a和结点b的距离,尽可能的大?”
“是的,并且我认为这两个结点会是以t为根结点的子树中深度最深的叶子结点l和以t为根结点的子树中不与l在t的同一棵子树中且深度最深的叶子结点l2。”小Hi道。
小Hi喝了口水,继续道:“我要想证明的结论是这样的——对于任意以t为根结点的子树中的两个结点l'和l2'(当然它们与t的连接路径上不能存在重合),一定满足dist(t, l')+dist(t, l2')<=dist(t, l)+dist(t, l2)。如果这个结论得到了证明,就意味着l和l2之间的路一定是最长路,或者说,不会有其它两个结点之间的距离比l和l2之间的距离更长了。”。
“并且这个证明非常简单——分情况讨论即可,如果l和l'在t的同一棵子树中,那么l2',l2肯定都不在这棵子树中——不然路径会发生重合,那么根据l,l',l2,l2'的定义,一定有dist(t, l)>=dist(t, l'),dist(t, l2)>=dist(t, l2'),于是我所想要的结论便得到了证明。”
“而如果l和l2'在t的同一棵子树中的话,这种情况就会和之前的那种一样。”
“那么接下来只有一种可能——l和l'不在t的同一棵子树中同时l和l2'不在t的同一棵子树中,首先我们可以知道dist(t, l)>=dist(t, l2),不然就与l与l2的定义矛盾了。其次我们知道dist(t, l2)>=dist(t, l'), dist(t, l2)>=dist(t, l2')——不然就与l2的定义矛盾了,那么显然便有dist(t, l')+dist(t, l2')<=dist(t, l2)+dist(t, l2)<=dist(t, l)+dist(t, l2)——也就是我们之前的结论得到了证明。”小Hi说到这里,抹了把汗,停下来看向小Ho。
“等……等……让我自己好好想想……”小Ho晕晕的拿出了纸币,自己演算了会,终于抬起头道:“没错,如果我知道了这个转折点t,那么我就可以用这样的方式找出最长路的两个端点来。”
小Ho言罢又想了想,继续问道:“那么我该怎么知道t是哪一个点呢?”
“好问题!而这个问题的答案是——枚举!”小Hi答道。
“枚举?”
“没错,我枚举每一个点作为转折点t,求出以t为根节点的子树中的‘最长路’以及与‘最长路’不重合的‘次长路’,用这两条路的长度之和去更新答案,那么最终的答案就是这棵树的最长路长度了!”小Hi道。
“但是……你这样做难道不是O(N^2)的复杂度么?”小Ho忍不住问道:“数据范围可是10^6啊!怎么可能算得出来。”
小Hi点了点头,答道:“所以就要利用一种神奇的性质了——如果我用first(t),second(t)分别表示以t为根节点的子树中最长路和次长路的长度,那么我只需要求出t的所有子结点的first值,first(t)便是这些first值中的最大值+1,second(t)便是这些first值中的次大值+1.”
“原来是这样,也就是说我只要以类似后序遍历的方式依次访问每个结点,从下往上依次计算每个结点的first值和second值,我就能够用O(N)的时间复杂度来解决这个问题咯!”
“是的呢!所以快去写程序吧~~”
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct Node {
int e,nxt;
}node[200005];//数组模拟链表
int n,num,ans;
int h[100005];
void add(int s,int e) {//加边
node[++num].e=e;
node[num].nxt=h[s];
h[s]=num;
}
int dfs(int u,int pre) {
int i=h[u],d,fir=0,sec=0;
while(i) {
if(node[i].e!=pre) {//因为是树,所以只用判断当前节点的前一个节点是否与其下一个节点相同
d=dfs(node[i].e,u)+1;
if(d>fir)//如果子树的本次最长路径大于目前最长路径,更新最长路径长度和次长路径长度
sec=fir,fir=d;
else if(d>sec)//如果子树的本次最长路径仅大于目前次长路径,更新次长路径长度
sec=d;
}
i=node[i].nxt;
}
ans=max(ans,fir+sec);//更新树的直径
return fir;
}
int main() {
int s,e,i;
while(1==scanf("%d",&n)) {
memset(h,0,sizeof(h));
ans=num=0;
for(i=1;i<n;++i) {
scanf("%d%d",&s,&e);
add(s,e);
add(e,s);
}
dfs(1,0);
printf("%d\n",ans);
}
return 0;
}