划分树
划分树
以下是我在学习了一上午划分树之后，自己对划分树的一点理解。
借助于（这儿有个传送门→）POJ 2104的代码来说一说划分树。
划分树的每一个节点都保存将输入的N个数，且保持顺序不变，作为根节点。
借助sort将原N个数升序排列，目的是要算出这N个数中间位置的数作为mid。
下面是划分树的节点结构定义：
int sor[maxn];//借助sort排序的数组
struct node
{
int num[maxn];//当前层的数
int cnt[maxn];
//cnt[]数组是划分树的核心部分
//保存每一个元素的左边的元素中位于下一层左子树的个数
} tree[40];//40是树的层数
建树的过程是一个递归过程，类似于快速排序。将小于mid的数放到左边，大于mid的数放到右边，这样二分后继续递归划分直到排序完毕，每次递归后小区间内必然都是有序的。
其中要注意的是，有可能出现与mid值重复的数，处理办法是先在mid的左边遍历一遍，把重复的数的数目记录下来，遇到的时候把这些数都放到左子树。
cnt数组是核心部分！保存每一个元素的左边的元素中位于下一层左子树的个数。
下面模拟建树过程：
举个栗子：
输入：1 5 2 6 3 7 4
sort后：1 2 3 4 5 6 7
得到第0层，即d=0时，mid=4。
第一行是输入的7个数，第二行是这七个数对应的cnt值。
d表示树的层数，d=0作为根，是原来输入的数组，以中间数mid为基准划分。
d=0 [1 5 2 6 3 7 4]mid=4
d=1 [1 2 3 4] mid=2 [5 6 7]mid=6
d=2 [1 2]mid=1 [3 4] mid=3 [5 6] mid=5 [7]
d=3 [1][2] [3][4] [5][6] [7]
划分完毕后：
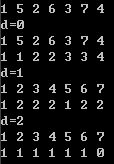第d层的第一行是划分后的7个数，第二行是这七个数对应的cnt值。
举个别的栗子帮助理解：
输入：2 4 3 5 8 1 7 6
sort后：1 2 3 4 5 6 7 8
得到第0层，即d=0时，mid=4。
d=0 [2 4 3 5 8 1 7 6]mid=4
d=1 [2 4 3 1] mid=2 [5 8 7 6]mid=6
d=2 [1 2]mid=1 [3 4] mid=3 [5 6] mid=5 [7 8]mid=7
d=3 [1][2] [3][4] [5][6] [7][8]
建树代码如下：
void buildtree(int l, int r, int d)//d是深度
{
if (l == r)//递归出口
{
return;
}
int mid = (l+r)>>1;//划分左右区间
int opleft = l, opright = mid+1;//对左右子树的操作位置的初始化
int same_as_mid = 0;//和sor[mid]相同的数的数目
//计算在mid左边有多少个和sor[mid]相同的数（包括mid）,都要放到左子树
for (int i = mid; i > 0; i--)
{
if (sor[i] == sor[mid])
same_as_mid++;
else
break;
}
int cnt_left = 0;//被划分到左子树的个数
for (int i = l; i <= r; i++)
{
//从l到r开始遍历
if (tree[d].num[i] < sor[mid])//左
{
tree[d+1].num[opleft++] = tree[d].num[i];
cnt_left++;
tree[d].cnt[i] = cnt_left;
}
else if(tree[d].num[i] == sor[mid] && same_as_mid)
{
//相同的都放在左子树
tree[d+1].num[opleft++] = tree[d].num[i];
cnt_left++;
tree[d].cnt[i] = cnt_left;
same_as_mid--;
}
else//右
{
tree[d].cnt[i] = cnt_left;
tree[d+1].num[opright++] = tree[d].num[i];
}
}
//递归建树
buildtree(l, mid, d+1);
buildtree(mid+1, r, d+1);
}
下面是查询过程。
注意到前面我们说，cnt数组保存每一个元素的左边的元素中位于下一层左子树的个数。
如果我们询问从区间[ql,qr]中第k小的数，然后我们通过cnt数组，确定[ql,qr]区间内有多少个点在下一层分入了左子树，然后判断第k数在左/右子树，然后递归查询。
步骤如下：
1、确定[ql,qr]区间内有多少个点在下一层分入了左子树：
在当前[ql,qr]区间内：如果ql是节点的左边界的话就有cnt[qr]个数进入左子树；否则，有m = cnt[qr] - cnt[ql-1]个数进入了左子树。
2、判断第k数在左/右子树：
①如果m <= k,，进入左子树查询第k数；
②否则，进入右子树查询k-m数。
3、确定在子树中查询的边界
int sum_in_left;//区间内元素位于下一层左子树的个数
int left;//[l,ql-1]左边的元素中位于下一层左子树的个数
①要找的点在左子树
如果在ql的左边有left个进入左子树，那么ql到qr中第一个进入左子树的必定在l+left的位置，所以此时新的区间范围：
int new_ql = l+left;
int new_qr = new_ql+sum_in_left-1;
②要找的点在右子树
int a = ql - l - left;//表示当前区间左半部分即[l,ql-1]中在下一层是右孩子的个数
int b = qr - ql + 1 - sum_in_left;//表示当前区间右半部分即[ql,qr]中在下一层是右孩子的个数
所以此时新的区间范围：
int new_ql = mid + a + 1;
int new_qr = mid + a + b;
查询的代码如下：
int query(int l, int r, int d, int ql, int qr, int k)
//1 n 0 a b k
//在d层[l,r]的节点里查找[a,b]中的第k大值
{
if (l == r)//递归出口
return tree[d].num[l];
int mid = (l+r)>>1;
int sum_in_left;//区间内元素位于下一层左子树的个数
int left;//[l,ql-1]左边的元素中位于下一层左子树的个数
if (ql == l)
{//如果ql是节点的左边界则有cnt[qr]个数进入左子树
sum_in_left = tree[d].cnt[qr];
left = 0;
}
else
{//如果ql不是节点的左边界则有cnt[qr]-cnt[ql-1]个数进入了左子树
sum_in_left = tree[d].cnt[qr] - tree[d].cnt[ql-1];
left = tree[d].cnt[ql-1];
}
if (sum_in_left >= k)
{//要找的点在左子树
//确定下一步询问的位置：
//如果在ql的左边有left个进入左子树
//那么ql到qr中第一个进入左子树的必定在l+left的位置
int new_ql = l+left;
int new_qr = new_ql+sum_in_left-1;
return query(l, mid, d+1, new_ql, new_qr, k);
}
else//要找的点在右子树
{
//确定下一步询问的位置
int a = ql - l - left;//表示当前区间左半部分即[l,ql-1]中在下一层是右孩子的个数
int b = qr - ql + 1 - sum_in_left;//表示当前区间右半部分即[ql,qr]中在下一层是右孩子的个数
int new_ql = mid + a + 1;
int new_qr = mid + a + b;
//k-sum_in_left表示要减去区间里已经进入左子树的个数
return query(mid+1, r, d+1, new_ql, new_qr, k - sum_in_left);
}
}