基于Spark实现的超大矩阵运算

由于标题强调了是在Spark平台实现的矩阵运算，所以本文会非常有针对性的介绍，甚至细节到Spark RDD的算子。

1.算法描述

思想其实很简单，就是矩阵分块计算，而分块矩阵就成了小矩阵，然后就借助于Breeze实现。而对于Spark平台而言，其处理流程如下图：

2.矩阵分块依据

这里仅仅提供一种思路，所以仅供参考。假设有两个矩阵A和B，其中A是m*k的矩阵，B是k*n的矩阵，CPU的总核数是cores，则分块方法：

• m > k && m > n --> m/2 && cores/2
• k > m && k > n --> k/2 && cores/2
• n > k && n > m --> n/2 && cores/2

3.分块矩阵ID标识：BlockID

由于BlockID最后要依靠RDD在集群中通信传输，所以BlockID必须是可序列化的。另外，BlockID要作为分块矩阵的唯一标识，所以BlockID必须具有唯一性，而BlockID的唯一由一下3个属性确定：

• blockRow：表示该子/分块矩阵在原矩阵中的行号；
• blockCol：表示该子/分块矩阵在原矩阵中的列号；
• blockSeq：表示该子/分块矩阵的序列号，默认为0。

4.矩阵分块原理

由于Spark处理文件时，是一行一行的处理的，所以一开始读文件，构成的RDD的类型是：RDD[(seqnum, DenseVector)] （seqnum:输入的行号，DenseVector:对应seqnum的矩阵行）。同时，我们还需要知道2个数据：

• allrow：矩阵的总行数
• allcol：矩阵的总列数

另外，由于矩阵运算中，矩阵形状的不同，所以分块的方式也随之而异。如下图，左上图就需要按列分块，右上图就需要按行分块，左下图就需要行列都分块，右下图就需要分别按列分块和按行分块。

4.1按行分块，列不分块

这时需要知道以下2个数据：

• rowblocknum：按行分块的数量
• subrow：每块矩阵的行数

然后，分三步处理：

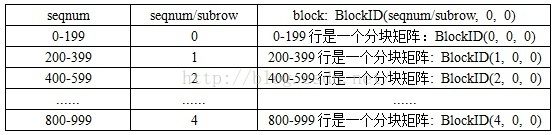
①mapPartitions{map}将RDD[(seqnum, DenseVector)]组成新的数据结构：RDD[(seqnum/subrow, (seqnum, DenseVector))]
②groupByKey作用RDD[(seqnum/subrow, (seqnum, DenseVector))]得到新的数据结构RDD[(seqnum/subrow, Iterable[(seqnum, DenseVector)])]

e.g.
allrow = 1000, rowblocknum = 5, subrow = allrow/rowblocknum = 200

③mapPartitions{map}把Iterable[(seqnum, DenseVector)]的数据填装到子/分块矩阵submatrix中
④构建新的数据结构：RDD[(BlockID, submatrix)]

4.2按行按列分块，和按列分块行不分

这时，我们需要知道3个数据，和准备一个存储行向量的数组：

• element: Array 读入的每行数据
• subcol: 每块矩阵的列数
• colblocknum：按列分块的数量
• arrayBuff: ArrayBuffer[(BlockID, (Long, Vector))] 存储按列切分的行向量

①mapPartitions{flatMap}将输入的每行数据按列切分，存储到arrayBuff: ArrayBuffer[(BlockID, (Long, Vector))]
②groupByKey作用RDD[(BlockID, (Long, Vector))]得到新的数据结构RDD[(BlockID, Iterable[(seqnum, DenseVector)])]
e.g.
allrow = 1000, rowblocknum = 5, subrow = allrow/rowblocknum = 200
allcol = 1000, colblocknum = 5, subcol = allcol/colblocknum = 200

③mapPartitions{map}把Iterable[(seqnum, DenseVector)]的数据填装到子/分块矩阵submatrix中
④构建新的数据结构：RDD[(BlockID, submatrix)]

5.矩阵乘法的例子

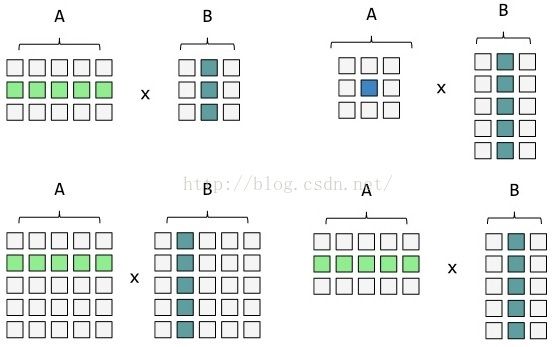
例如：有两个矩阵A和B，其中A是6m*4k的矩阵，被分为3*2块个子矩阵；B是4k*4n的矩阵，被分为2*2块的子矩阵。如图：

下标(x,y,z)是每个子/分块矩阵的唯一标识BlockID(row: Int, col: Int, seq: Int = 0)的参数，即：

• x：表示该子/分块矩阵在原矩阵中的行号，即blockRow；
• y：表示该子/分块矩阵在原矩阵中的列号，即blockCol；
• z：表示该子/分块矩阵的序列号，默认为0，即blockSeq。

和分块块数：

• mSplitNum：表示矩阵A按行切分的块数；
• kSplitNum：表示矩阵A按列切分的块数，也是矩阵B按行切分的块数；
• nSplitNum：表示矩阵B按列切分的块数。

对于该例子，mSplitNum=3、kSplitNum=2、nSplitNum=2。
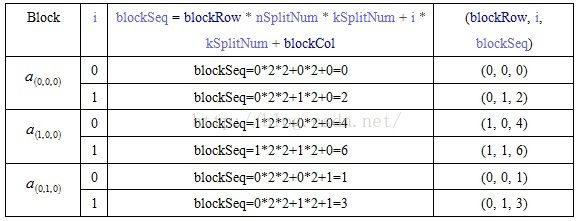
①mapPartitions{flatMap}把RDD[(BlockID, submatrix)]，即矩阵A的每个子/分块矩阵按序列号生成nSplitNum个RDD[(BlockID, submatrix)]，矩阵B的每个子/分块矩阵按序列号生成mSplitNum个RDD[(BlockID, subMatrix)]，使之一一对应。
对于矩阵A

val array = Array.ofDim[(BlockID, DenseMatrix[Double])](nSplitNum)
    for (i <- 0 until nSplitNum) {
         val blockSeq = blockRow * nSplitNum * kSplitNum + i * kSplitNum + blockCol
         array(i) = (new BlockID(blockRow, i, blockSeq), DenseMatrix)
}

对于矩阵B

val array = Array.ofDim[(BlockID, DenseMatrix [Double])](mSplitNum)
    for (i <- 0 until mSplitNum) {
         val blockSeq = i * nSplitNum * kSplitNum + blockCol * kSplitNum + blockRow
        array(i) = (new BlockID(i, blockCol, blockSeq), DenseMatrix)
}

e.g. mSplitNum=3，kSplitNum=2，nSplitNum=2
MatrixA

MatrixB

即：MatrixA每个子/分块矩阵复制nSplitNum份，MatrixB每个子/分块矩阵复制mSplitNum份，然后把Key值BlockID相同的子/分块矩阵相乘。
②join两矩阵A和B，使每一对subMatrix相乘，同时更新BlockID(blockRow, blockCol)使blockSeq默认为0。
③reduceByKey按BlockID把子/分块矩阵的乘积相加，得到最终的矩阵。

声明：这只是个人思想，仅做参考。按照这个想法，如果不做任何优化（比如，相乘的小矩阵不分块，而是采用广播的方式等等），在我的实验集群中好像最多能处理10000*10000*10000规模的数据集。

参考文献：

http://www.open-open.com/doc/view/dc6d0ce0233d4db397fd677a2d0a55dc