【LeetCode】003 Unique Paths 唯一路线
【题目】
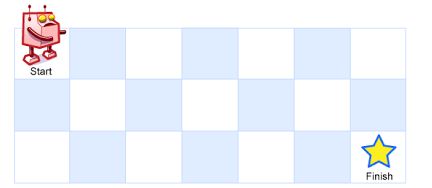
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
m×n的方阵,从左上到右下一共有多少种走法?(只能左移下移)
【解析】
思路一:(嵌套,自古嵌套多费时)
每移动一步,机器人有两种选择,可以看成方阵减少了一行(或一列),当方阵行数或者列数为1时,只有一种路线到达最右。
程序如下:
int uniquePaths(int m, int n) {
if(m>1 && n>1)
return uniquePaths(m-1,n) + uniquePaths(m,n-1);
else
return 1;
}
毫无疑问的超时了,没有测试结果的正确性,但是我认为这种思路应该没错。
思路二:排列组合
到达目的地一共需要m+n-2步,其中向右走为n-1步,向下走为m-1步。
假设,现有两个篮子,一个篮子为向左走,一个篮子为向右走。有m+n-2个带有编号的球,编号为1……i……m+n-2,代表第i步。编号为i的球扔进对应的篮子里,代表第i步向右或者向下走。现将m+n-2个球中挑选n-1个球扔进“右”篮子中,其余m-1个球扔进“下”篮子中。
以上组合方式的数量即为总共的路径数,即:C(n-1,m+n-2)
算法已经出来了,接下来就是语法。这个过程也是让我头疼了好一会呢。
起初,使用分子分母分别计算出来,再相除,return结果的方法,100!数字太大溢出。
错误程序如下:
int uniquePaths(int m, int n) {
int M = m+n-2;
int N = n-1;
long A=1, B=1;
while(N)
{
A *= M--;
B *= N--;
}
return A/B;
}
后来,使用先分子分母相除 再将结果相乘 出现精度问题。
语句 ans *= (double)(M--)/(N--) 中,若不使用double转换变量类型,则会在相除过程中抹去小数部分。(int)(ans+0.5) ,加上0.5在转换为int型 即能满足四舍五入的要求,保证了精度。
程序如下:
int uniquePaths(int m, int n) {
int M = m+n-2;
int N = n-1;
double ans=1;
while(N)
ans *= (double)(M--)/(N--);
return (int)(ans+0.5);
}
【程序】
没闹明白为什么它就没有出现精度问题。我的最后一步没有四舍五入的话,有的测试数据会有1的误差。