他山之石,可以攻玉。除了辅之以不同的颜色、符号外,散点图中还可以添加其他图形元素,以增强表达力,最常见的添加剂有坐标轴须、直方图、箱线图、平滑曲线、拟合曲线等。
常见的画散点图矩阵的函数有:
-
pairs(graphics)
R中,graphics包中的pairs()是画散点图矩阵的长老级函数,它不仅可以绘制最朴素的散点图矩阵,同时也可以通过进一步设置绘图参数进行配置(参见?pairs),达到更高的要求(添加其他图形元素等)。不过进一步设置较为麻烦,幸好后面要介绍的函数已经可以满足我们常见的额外要求。
以鸢尾花数据为例,用以下代码绘制其散点图(图1),不同颜色分别代表不同品种的鸢尾花。
pairs(iris[1:4], main = "Anderson's Iris Data -- 3 species",
pch = 21,
bg = c("red", "green3", "blue")[unclass(iris$Species)])
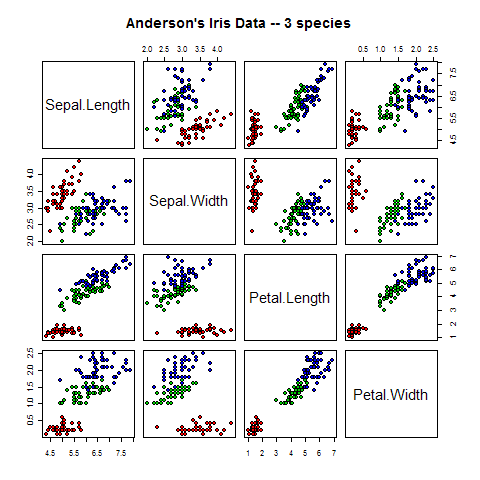 图1 pairs
图1 pairs
实际上,图1已经可以给我们很多信息,包括各类鸢尾花的花瓣、花萼长宽的大体分布以及它们两两之间的关系。
-
scatterplot.matrix(car)
car包中的scatterplot.matrix()函数(可以简写为spm())可以直接指定散点图中主对角线上的绘图元素(密度图、箱线图、直方图、QQ图等),还可以在散点图中添加拟合曲线、平滑曲线、相关读椭圆等。
同样利用鸢尾花数据,下面代码画出其散点图矩阵(图2).
library(car)
spm(~Sepal.Length + Sepal.Width + Petal.Length + Petal.Width |
Species, data = iris)
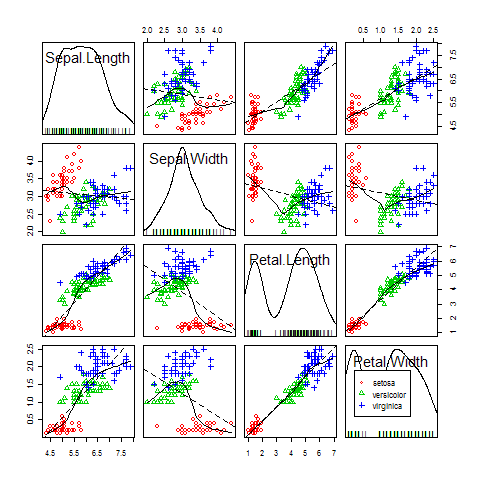 图2 spm
图2 spm
-
gpairs(YaleToolkit)
YaleToolKit包中的gpairs()函数同样可以绘制散点图矩阵,较之spm()函数,它更为复杂一些。下面代码得到图3,更多的例子参见帮助文档。
library(YaleToolkit)
gpairs(iris, upper.pars = list(scatter = 'stats'),
scatter.pars = list(pch = 1:3,
col = as.numeric(iris$Species)),
stat.pars = list(verbose = FALSE))
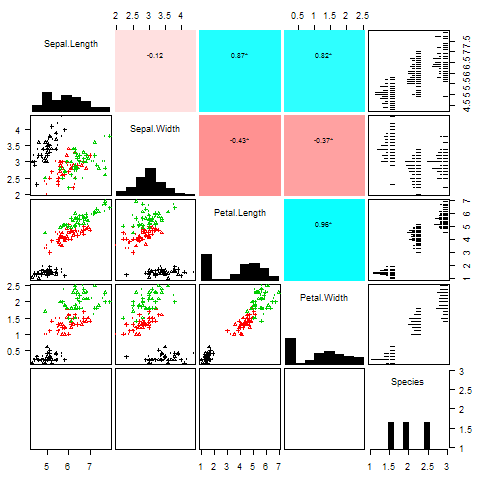 图3 gpairs
图3 gpairs
-
splom(lattice)
lattice包是基于网格系统的,是S-PLUS里的Trellis图形在R中的实现。Trellis是多元数据可视化的方法,特别适用于发现各变量之间的相互作用关系。Lattice(Trellis)的主要想法是不同条件下的多个图:根据某变量的值的不同对两个变量作不同图。
lattice包中的splom()函数可以按类别绘制散点图矩阵,也可以通过进一步的设置达到更高的要求。下面的代码再次得到鸢尾花数据的散点图矩阵(图4)。
library(lattice)
super.sym <- trellis.par.get("superpose.symbol")
splom(~iris[1:4], groups = Species, data = iris,
panel = panel.superpose,
key = list(title = "Three Varieties of Iris",
columns = 3,
points = list(pch = super.sym$pch[1:3],
col = super.sym$col[1:3]),
text = list(c("Setosa", "Versicolor", "Virginica"))))
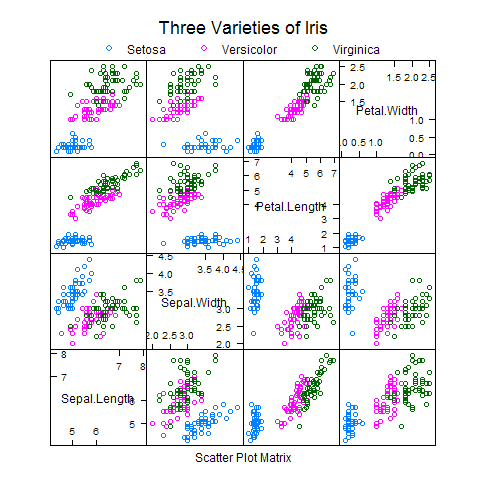 图4 splom
图4 splom
讨论
益辉曰:
曾经有人问我认为什么统计方法最好,我不假思索地回答,‘散点图’ 呗!当然,这里面也有开玩笑的成份,但意思也是想表达统计方法的应用,应该能让人家容易理解你的意图。
散点图直观明了,是一类重要的可视化方法。以上文字仅仅简要介绍了四个绘制散点图矩阵的函数,很是粗糙,具体的细节还需要进一步阅读帮助文档。
本文的首要目的是提醒大家可以让散点图矩阵如虎添翼,主要是与其他图形(触须图、直方图、箱线图、平滑线、拟合线等)的适当搭配;第二目的是希望大家通过上面的介绍,可以选择自己需要的绘图函数,从而省去一些不必要的探索时间。