PKU Campus 2010 (POJ Monthly Contest – 2010.05.09) 部分解题报告

PKU 3761  A题：公式题，推不出来； http://162.105.81.212/JudgeOnline/problem?id=3761

PKU 3762  B题：比赛时候没怎么看，也受了点额外影响。。。，比赛后听说是费用流，然后仔细看了下题，发现还真是，先将时间转化成对应的点，范围必在0~(23*3600+59*60+59) 之中，显然这样直接建图会TLE，所以必须离散化，离散化这里可以用二分，不过这里最多只有86399次不用也无所谓，然后按时间点先后连一条边流量为k，费用为0，对于每个工作对应两个时间点，两个时间点连一条流量为1，费用为w的边；然后建立源点s和汇点t，s连1，最后点nodenum连t；费用流模板就好了，但是这里手写队列的时候我开小了，re了很多次。。。 http://162.105.81.212/JudgeOnline/problem?id=3762  

代码：

#include<stdio.h> #include<string.h> const int N = 4011 ; int hash[86411]; int n,k,en,s,t,maxflow,nodenum; struct node { int from,to,cost; }E[2011]; struct Node { int vdx,flow,cost,opp,next ; }Edge[N*4]; int indx[N],road[N],pre[N],used[N],dis[N],all[1000*N]; void add(int from,int to,int flow,int cost) { Edge[en].vdx = to ; Edge[en].flow = flow ; Edge[en].cost = cost ; Edge[en].opp = en+1 ; Edge[en].next = indx[from] ; indx[from] = en++ ; Edge[en].vdx = from ; Edge[en].flow = 0 ; Edge[en].cost = -cost ; Edge[en].opp = en-1 ; Edge[en].next = indx[to] ; indx[to] = en++ ; } bool spfa() { for(int i=1;i<=t;i++) used[i] = 0 , dis[i] = -1 ; used[s] = 1 , dis[s] = 0 ; int head = 0 , tail = 0 ; all[tail++] = s ; while(head < tail) { int u = all[head++] ; used[u] = 0 ; for(int ptr=indx[u];ptr!=-1;ptr=Edge[ptr].next) { int v = Edge[ptr].vdx ; if(Edge[ptr].flow>0 && dis[v] < dis[u]+Edge[ptr].cost) { dis[v] = dis[u]+Edge[ptr].cost ; pre[v] = u ; road[v] = ptr ; if(!used[v]) { used[v] = 1 ; all[tail++] = v ; } } } } if(dis[t]==-1) return false ; return true ; } void argue() { for(int v=t;v!=s;v=pre[v]) { maxflow += Edge[road[v]].cost ; Edge[road[v]].flow -- ; Edge[Edge[road[v]].opp].flow ++ ; } } int main() { while(~scanf("%d%d",&n,&k)) { int a,b,c,tmp; memset(hash,0,sizeof(hash)) ; nodenum = 1 ; for(int i=1;i<=n;i++) { scanf("%d:%d:%d",&a,&b,&c); tmp = a*3600 + b*60 + c ; E[i].from = tmp ; if(!hash[tmp]) { hash[tmp] = 1 ; nodenum++ ; } scanf("%d:%d:%d",&a,&b,&c) ; tmp = a*3600 + b*60 + c ; E[i].to = tmp ; if(!hash[tmp]) { hash[tmp] = 1 ; nodenum++ ; } scanf("%d",&E[i].cost) ; } int m = 1 ; for(int i=0;i<86400;i++) { if(hash[i]) { hash[i] = m++ ; if(m==nodenum) break ; } } s = nodenum,t = nodenum+1 ; for(int i=1;i<=t;i++) indx[i] = -1 ; for(int i=1;i<nodenum-1;i++) add(i,i+1,k,0) ; for(int i=1;i<=n;i++) { a = hash[E[i].from] ; b = hash[E[i].to] ; add(a,b,1,E[i].cost) ; } nodenum -- ; add(s,1,k,0); add(nodenum,t,k,0); maxflow = 0 ; while(k-- && spfa()) argue() ; printf("%d/n",maxflow); } return 0 ; }

PKU 3763 C题，树形DP：在一棵树上添加多少条边，可以是得他构成哈密顿回路；http://162.105.81.212/JudgeOnline/problem?id=3763

这样考虑，我们只要把一棵树添加一些边变成一条路径数量为k，那么在添加一条边使首尾相接即可，那么答案及是 k+1 ；

对于一棵子树；我们有两种方案去添边，比如一个子树；

1 2

1 3

1 4

1 5 ；

那么我们有方案1：以树根1为一条链的起点，1-2 ，那么其他的链就是 3 ，4 ，5 ，要想它连成一条链就得添加2-3，3-4,4-5这两条边；

               方案2：以子树的一个儿子为起点，另一个儿子为终点的链为，2-1-3，其他链为4,5，要添加3-4,4-5，才构成一条路径；

那么针对上述的情况有状态：

dp[u][0],表示以u为根节点，u必定是链的一端的最少需要边数；

dp[u][1],表示以u为根节点，u不一定是链的一端，可以是端点也可以是中间点的  所需添加的最少边数；

转移：

tot 表示以u为除v外树根的儿子dp[v][1] ;

dp[u][0] = min{dp[u][o],dp[v][0]+tot+son[u]-1} ;

dp[u][1] = min{dp[u][1],dp[x][0]+dp[y][0]+tot+son[u]-2} ;

dp[u][1] = min{dp[u][1],dp[u][0]};

代码：
#include<stdio.h> #include<string.h> #include<algorithm> using namespace std ; const int N = 100001 ; const int Inf = 100000000 ; struct Node { int vdx ; Node *next ; }*map[N],nome[2*N] ; int n,en; void add(int from,int to) { Node *ptr = &nome[en++] ; ptr ->vdx = to ; ptr ->next = map[from] ; map[from] = ptr ; } int son[N],dp[N][2],sug[N]; bool used[N] ; int cmp(int a,int b) { return dp[a][0]-dp[a][1] < dp[b][0]-dp[b][1] ; } void dfs(int u,int f) { int v , tot = 0 ; used[u] = true ; dp[u][0] = dp[u][1] = Inf ; for(Node *ptr=map[u];ptr;ptr=ptr->next) { v = ptr -> vdx ; if(!used[v]) { son[u] ++ ; dfs(v,u) ; tot += dp[v][1] ; } } if(son[u] == 0) { dp[u][0] = dp[u][1] = 0 ; return ; } int j = 0 ; for(Node *ptr=map[u];ptr;ptr=ptr->next) { int v = ptr -> vdx ; if(v != f) { dp[u][0] = min(dp[u][0],tot-dp[v][1]+dp[v][0]+son[u]-1) ; sug[j++] = v ; } } sort(sug,sug+j,cmp) ; if(j==1) { dp[u][1] = dp[u][0] ; }else { int x = sug[0] , y = sug[1] ; dp[u][1] = tot - dp[x][1] - dp[y][1] + dp[x][0] + dp[y][0] + son[u]-2 ; dp[u][1] = min(dp[u][0],dp[u][1]) ; } } int readT() { char c;int ret; while(c=getchar(),c<'0'||c>'9'); ret=c-'0'; while(c=getchar(),c>='0'&&c<='9')ret=ret*10+c-'0'; return ret; } int main() { while(~scanf("%d",&n)) { int a,b ; en=0; for(int i=1;i<=n;i++) map[i] = NULL ; for(int i=1;i<n;i++) { a = readT() ; b = readT() ; add(a,b) ; add(b,a) ; } memset(son,0,sizeof(son)) ; memset(used,false,sizeof(used)) ; dfs(1,-1) ; printf("%d/n",dp[1][1]+1) ; } return 0 ; }

PKU 3764  http://162.105.81.212/JudgeOnline/problem?id=3764

D题：这是到好题，实际上就是dfs一遍，计算出从根到每个点i的xor路径值a[i]，然后找出一对i,j使得a[i] xor a[j]最大 ；

主要是后面求一对i,j的时候有些问题；

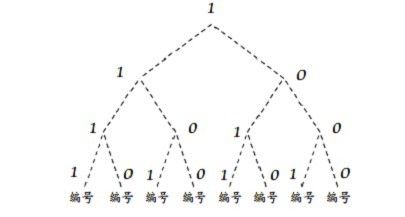
这里用到一个算法，建立一个0 1二叉树，对于当前的一个数，把他添加到这个树上，依次把这每个数添加到这棵树上，然后在这棵树上贪心求最大值，贪心的正确性请参考09年武森的论文中的Cow Xor例题；

01二叉树：

一个节点的左孩子边为1，右孩子边位0；

然后就是插入；

 

 最后没插入一个数，这样贪心的访问一次好了。。

代码：

 

#include<stdio.h> #include<string.h> #include<algorithm> using namespace std ; const int N = 100001 ; struct Node { int vdx ; int cost ; Node *next ; }*map[N],nome[2*N] ; int n,en,root,Max,Xor[N] ; void add(int from,int to,int cost) { Node *ptr =&nome[en++] ; ptr -> vdx = to ; ptr -> cost = cost ; ptr -> next = map[from] ; map[from] = ptr ; } bool used[N] ; void dfs(int u) { used[u] = true ; if(Xor[u] >Max) Max = Xor[u] ; for(Node *ptr=map[u];ptr;ptr=ptr->next) { int v = ptr->vdx ; if(!used[v]) { if(u==root) Xor[v] = ptr->cost ; else Xor[v] = (ptr->cost^Xor[u]) ; dfs(v); } } } int readT() { char c;int ret; while(c=getchar(),c<'0'||c>'9'); ret=c-'0'; while(c=getchar(),c>='0'&&c<='9')ret=ret*10+c-'0'; return ret; } int chd[100000*31][2]; int zn,maxdeep = 30; int arr[32] ; void Insert() { int p = 0 ; for(int i=maxdeep;i>=0;i--) { if(chd[p][arr[i]]==-1) { memset(chd[zn],-1,sizeof(chd[zn])); chd[p][arr[i]] = zn ++ ; } p = chd[p][arr[i]] ; } } int query(int idx,int deep) { if(deep == -1) { return 0 ; } if(chd[idx][1-arr[deep]] != -1) { return (1<<deep) + query(chd[idx][1-arr[deep]],deep-1) ; }else { return query(chd[idx][arr[deep]],deep-1) ; } } int main() { while(scanf("%d",&n) != EOF) { int a,b,c; en = 0 ; for(int i=0;i<=n;i++) map[i] = NULL ; for(int i=1;i<n;i++) { a = readT() ; b = readT() ; c = readT() ; add(a,b,c) ; add(b,a,c) ; } Max = -1 ; memset(used,false,sizeof(used)); root = 0 ; Xor[root] = 0 ; dfs(root) ; memset(chd[0],-1,sizeof(chd[0])); zn = 1 ; for(int i=0;i<n;i++) { for(int j=maxdeep;j>=0;j--) { if(Xor[i]&(1<<j)) { arr[j] = 1 ; }else { arr[j] = 0 ; } } Insert() ; Max =max(Max,query(0,maxdeep)); } printf("%d/n",Max); } return 0 ; }   

E题：模拟题(水);

G题：dij (水);

H题：模拟题(水)；