网络安全常用数学定理

   费尔玛(Fermat)定理和欧拉(Euler)定理在公钥密码体制中起着重要作用。

1.费尔玛定理

    定理4 -2(Fermat)若 p 是素数 ,a 是正整数且gcd (a,p) =1 , 则 a p -1 ≡1 mod  p 。

2.欧拉函数

    设 n 是一正整数 , 小于 n 且与 n 互素的正整数的个数称为 n 的欧拉函数 , 记为φ (n)

   定理4-3若n是两个素数p和q的乘积,则φ(n)=φ(p)×φ(q)=(p -1)×(q-1)。

3.欧拉定理

    定理4 -4(Euler)若 a 和 n 互素 , 则 a φ (n) ≡1 mod  n

4.素性检验

    素性检验是指对给定的数检验其是否为素数。对于大数的素性检验来说没有简单直接的方法,本节介绍一个概率检验法,为此需要以下引理。
    引理如果p为大于2的素数,则方程x2≡1(mod p)的解只有x≡1和x≡-1

5.欧几里得算法

    欧几里得(Euclid)算法是数论中的一个基本技术,是求两个正整数的最大公因子的简化过程。而推广的Euclid算法不仅可求两个正整数的最大公因子,而且当两个正整数互素时,还可求出其中一个数关于另一个数的乘法逆元。

求最大公因子

    对任意非负整数a和正整数b,有gcd(a,b)=gcd(b,a mod b)

    例如:gcd(55,22)=gcd(22,55 mod 22)=gcd(22,11)=gcd(11,0)=1 1。

    在求两个数的最大公因子时,可重复使用以上结论。
    例如:gcd(18,12)=gcd(12,6)=gcd(6,0)=6,
    gcd(11,10)=gcd(10,1)=gcd(1,0)=1。

    Euclid算法就是用这种方法,因gcd(a,b)=gcd(|a|,|b|),因此可假定算法的输入是两个正整数,设为d,f,并设f>d。

    Euclid(f,d)步骤：

    1.X←f;Y←d;
    2.if Y=0 then return X=gcd(f,d);
    3.R=X mod Y;
    4.X=Y;
    5.Y=R;
    6.goto 2。

求乘法逆元
   如果gcd(a,b)=1,则b在mod a下有乘法逆元(不妨设b<a),即存在一x(x<a),使得b x≡1 mod a。推广的Euclid算法先求出gcd(a,b),当gcd(a,b)=1时,则返回b的逆元。

6.中国剩余定理

中国剩余定理是数论中最有用的一个工具,定理说如果已知某个数关于一些两两互素的数的同余类集,就可重构这个数。

例如:Z10中每个数都可从这个数关于2和5(10的两个互素的因子)的同余类重构。比如已知x关于2和5的同余类分别是[0]和[3],即x mod 2≡0,x mod 5≡3。可知是偶数且被5除后余数是3,所以可得8是满足这一关系的惟一的x。

中国剩余定理：设m1,m2,…,mk是两两互素的正整数,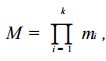则一次同余方程组

对模M有惟一解:

其中ei满足:.

由以下方程组求x。
   x≡1 mod 2
   x≡2 mod 3
   x≡3 mod 5
   x≡5 mod 7

解:M=2·3·5·7=210,令Mi=M/mi,M1=105,M2=70,M3=42,M4=30,易求

e1≡M1-1 mod 2≡1,e2≡M2-1 mod 3≡1,e3≡M3-1 mod 5≡3,e4≡M4-1 mod 7≡4,所以
   x mod 210≡(105×1×1+70×1×2+42×3×3+30×4×5)mod 210≡173,或写成x≡173 mod 210。

 

本文地址：http://blog.csdn.net/a359680405/article/details/41890619