Wunder Fund Round 2016 (Div. 1 + Div. 2 combined)(A、B、C、D)题解
A. Slime Combining
Your friend recently gave you some slimes for your birthday. You have n slimes all initially with value 1.
You are going to play a game with these slimes. Initially, you put a single slime by itself in a row. Then, you will add the other n - 1 slimes one by one. When you add a slime, you place it at the right of all already placed slimes. Then, while the last two slimes in the row have the same value v, you combine them together to create a slime with value v + 1.
You would like to see what the final state of the row is after you’ve added all n slimes. Please print the values of the slimes in the row from left to right.
Input
The first line of the input will contain a single integer, n (1 ≤ n ≤ 100 000).
Output
Output a single line with k integers, where k is the number of slimes in the row after you’ve finished the procedure described in the problem statement. The i-th of these numbers should be the value of the i-th slime from the left.
Sample test(s)
Input
1
Output
1
Input
2
Output
2
Input
3
Output
2 1
Input
8
Output
4
Note
In the first sample, we only have a single slime with value 1. The final state of the board is just a single slime with value 1.
In the second sample, we perform the following steps:
Initially we place a single slime in a row by itself. Thus, row is initially 1.
Then, we will add another slime. The row is now 1 1. Since two rightmost slimes have the same values, we should replace these slimes with one with value 2. Thus, the final state of the board is 2.
In the third sample, after adding the first two slimes, our row is 2. After adding one more slime, the row becomes 2 1.
In the last sample, the steps look as follows:
1. 1
2. 2
3. 2 1
4. 3
5. 3 1
6. 3 2
7. 3 2 1
8. 4
题意:
有n个笑脸,值都是1,一个一个的放到一行上,如果最后两个笑脸的值一样,就将它们结合在一起,并且值加1。当n个笑脸都放上去的时候,输入这一行上存在的笑脸(从左往右输出)
思路:下面的代码是用模拟的方法,ans数组里存放的是这一行上的笑脸,每放上一个笑脸就判断有没有可以合并的,如果有可以合并的就合并在一起,然后继续放笑脸。
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#define N 100009
#define ll long long
const int INF = 0x3fffffff;
using namespace std;
int ans[N];
int main()
{
#ifndef ONLINE_JUDGE
// freopen("1.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
int i, j, k;
int n ;
cin >> n;
for (i = 0, j = 0; i < n; i++)
{
ans[j++] = 1;
for (k = j-1; k >= 1; k--)
{
if (ans[k] == ans[k-1])
{
ans[k-1]++;
j--;
}
else break;
}
}
for (i = 0; i < j; i++)
cout << ans[i] << ' ';
return 0;
}下面的代码是我hack别人时看到的,写得好简单。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
scanf("%d", &n);
for (int i = 20; i >= 0; i--)
if (n&(1<<i)) printf("%d ", i+1);
return 0;
}B. Guess the Permutation
Bob has a permutation of integers from 1 to n. Denote this permutation as p. The i-th element of p will be denoted as pi. For all pairs of distinct integers i, j between 1 and n, he wrote the number ai, j = min(pi, pj). He writes ai, i = 0 for all integer i from 1 to n.
Bob gave you all the values of ai, j that he wrote down. Your job is to reconstruct any permutation that could have generated these values. The input will be formed so that it is guaranteed that there is at least one solution that is consistent with the information given.
Input
The first line of the input will contain a single integer n (2 ≤ n ≤ 50).
The next n lines will contain the values of ai, j. The j-th number on the i-th line will represent ai, j. The i-th number on the i-th line will be 0. It’s guaranteed that ai, j = aj, i and there is at least one solution consistent with the information given.
Output
Print n space separated integers, which represents a permutation that could have generated these values. If there are multiple possible solutions, print any of them.
Sample test(s)
Input
2
0 1
1 0
Output
2 1
Input
5
0 2 2 1 2
2 0 4 1 3
2 4 0 1 3
1 1 1 0 1
2 3 3 1 0
Output
2 5 4 1 3
Note
In the first case, the answer can be {1, 2} or {2, 1}.
In the second case, another possible answer is {2, 4, 5, 1, 3}.
题意:
p数组是1~n,n个数字的一个排列,定义矩阵ai,j=min(pi, pj),ai, i=0;保证矩阵a是对称矩阵,求p数组,如果有多组,则随便输出一组
思路:
统计第i行各个数出现的次数,最多的那一个数就是p[i],如果所有的数字出现的次数都一样,则这个数可能是n,也可能是n-1
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#define N 55
#define ll long long
const int INF = 0x3fffffff;
using namespace std;
int a[N], n, ans[N], b[N];
int main()
{
#ifndef ONLINE_JUDGE
freopen("1.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
bool flag = false;
int i, j, k = 0, t, tt;
cin >> n;
memset(ans, 0, sizeof(ans));
for (i = 0; i < n; i++)
{
memset(a, 0, sizeof(a));
for (j = 0; j < n; j++)
{
cin >> b[j];
a[b[j]]++;
}
t = 0;
for (j = 1; j <= n; j++)
{
if (a[t] < a[j]) t = j;
}
if (t) ans[i] = t;
else
{
if (flag)
{
ans[i] = n;//第二次出现各个数出现次数都是1的时候
}
else
{
ans[i] = n-1;//第一次出现各个数出现次数都是1的时候
flag = true;
}
}
}
for (i = 0; i < n; i++)
cout << ans[i] << ' ';
return 0;
}C. Constellation
Cat Noku has obtained a map of the night sky. On this map, he found a constellation with n stars numbered from 1 to n. For each i, the i-th star is located at coordinates (xi, yi). No two stars are located at the same position.
In the evening Noku is going to take a look at the night sky. He would like to find three distinct stars and form a triangle. The triangle must have positive area. In addition, all other stars must lie strictly outside of this triangle. He is having trouble finding the answer and would like your help. Your job is to find the indices of three stars that would form a triangle that satisfies all the conditions.
It is guaranteed that there is no line such that all stars lie on that line. It can be proven that if the previous condition is satisfied, there exists a solution to this problem.
Input
The first line of the input contains a single integer n (3 ≤ n ≤ 100 000).
Each of the next n lines contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109).
It is guaranteed that no two stars lie at the same point, and there does not exist a line such that all stars lie on that line.
Output
Print three distinct integers on a single line — the indices of the three points that form a triangle that satisfies the conditions stated in the problem.
If there are multiple possible answers, you may print any of them.
Sample test(s)
Input
3
0 1
1 0
1 1
Output
1 2 3
Input
5
0 0
0 2
2 0
2 2
1 1
Output
1 3 5
Note
In the first sample, we can print the three indices in any order.
In the second sample, we have the following picture.
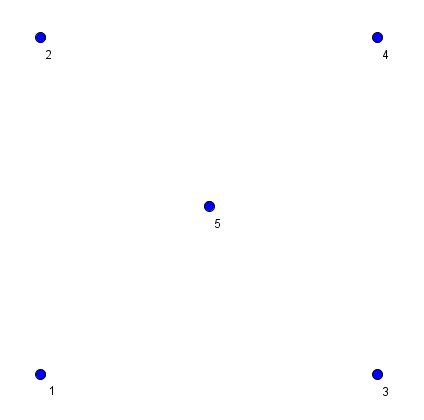
Note that the triangle formed by starts 1, 4 and 3 doesn’t satisfy the conditions stated in the problem, as point 5 is not strictly outside of this triangle (it lies on it’s border).
题意:
给n个点的坐标,要求输出三个点,要求这三个点可以构成一个三角形,且这个三角形内不能包含其他的点,如果有多种情况,则输出一种即可。
思路:
首先要明白 如何判断一个点是不是一个在三角形内部
首先,先排一下序,先按x排序,x一样的再按y排序。如果不排序就会出错,我的就是这样被hack的~~o(>_<)o ~~
(hack数据
5
0 0
2 0
1 0
1 1
1 -1)
一定可以找一个满足题意的三角形,使这个三角形包含第一个点和第二个点
用反证法证明,很好证明,画图便知,这里不做证明
这样我们就已经确定了两个点,我们只需从3到n遍历第三个点,首先判断这三个点是否能构成三角形,如果可以构成三角形,在遍历剩下的n-3个点是不是在三角形内。
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#define N 100005
#define ll long long
const int INF = 0x3fffffff;
using namespace std;
struct point
{
ll x, y, id;
friend bool operator < (point a, point b)
{
if (a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
}p[N];
int n;
ll area(point &a, point &b, point &c)
{
return (a.x-b.x)*(a.y+b.y)+(b.x-c.x)*(b.y+c.y)+(c.x-a.x)*(c.y+a.y);//如果是计算三角形的面积的话,还需要除2
//并取绝对值,这里只是判断abc是顺时针还是逆时针
//所以只需要符号就行,并不需要具体指
}
bool fun(point &a, point &b)//判断b是不是在a,p[0],p[1]构成的三角形内
{
ll x, y, z;
x = area(p[0], p[1], b);
if (!x)
{
if ((p[0].x-b.x)*(p[1].x-b.x) < 0) return true;
}
y = area(p[1], a, b);
if (!y)
{
if ((p[1].x-b.x)*(a.x-b.x) < 0) return true;
}
z = area(a, p[0], b);
if (!z)
{
if ((a.x-b.x)*(p[0].x-b.x) < 0) return true;
}
if (x > 0 && y > 0 && z > 0) return true;
if (x < 0 && y < 0 && z < 0) return true;
//x, y, z, 同号说明b在三角形a p[0] p[1]内
return false;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("1.txt", "r", stdin);
#endif
ll i, j, k;
bool flag;
scanf("%d", &n);
for (i = 0; i < n; i++)
{
scanf("%I64d%I64d", &p[i].x, &p[i].y);
p[i].id = i+1;
}
sort(p, p+n);
for (i = 2; i < n; i++)
{
k = area(p[0], p[1], p[i]);
if (!k) continue;
flag = true;
for (j = 2; j < n; j++)
{
if (j == i) continue;
if (fun(p[i], p[j]))
{
flag = false;
break;
}
}
if (flag)
{
printf("%I64d %I64d %I64d", p[0].id, p[1].id, p[i].id);
break;
}
}
return 0;
}D. Hamiltonian Spanning Tree
A group of n cities is connected by a network of roads. There is an undirected road between every pair of cities, so there are ![]() roads in total. It takes exactly y seconds to traverse any single road.
roads in total. It takes exactly y seconds to traverse any single road.
A spanning tree is a set of roads containing exactly n - 1 roads such that it’s possible to travel between any two cities using only these roads.
Some spanning tree of the initial network was chosen. For every road in this tree the time one needs to traverse this road was changed from y to x seconds. Note that it’s not guaranteed that x is smaller than y.
You would like to travel through all the cities using the shortest path possible. Given n, x, y and a description of the spanning tree that was chosen, find the cost of the shortest path that starts in any city, ends in any city and visits all cities exactly once.
Input
The first line of the input contains three integers n, x and y (2 ≤ n ≤ 200 000, 1 ≤ x, y ≤ 109).
Each of the next n - 1 lines contains a description of a road in the spanning tree. The i-th of these lines contains two integers ui and vi (1 ≤ ui, vi ≤ n) — indices of the cities connected by the i-th road. It is guaranteed that these roads form a spanning tree.
Output
Print a single integer — the minimum number of seconds one needs to spend in order to visit all the cities exactly once.
Sample test(s)
Input
5 2 3
1 2
1 3
3 4
5 3
Output
9
Input
5 3 2
1 2
1 3
3 4
5 3
Output
8
Note
In the first sample, roads of the spanning tree have cost 2, while other roads have cost 3. One example of an optimal path is ![]() .
.
In the second sample, we have the same spanning tree, but roads in the spanning tree cost 3, while other roads cost 2. One example of an optimal path is ![]() .
.
题意:
有一个n个点的无向完全图,共![]() 条边,给出一个图中的一个生成树。在生成树上的权值是x,其他地方的权值是y,问不重复的变量完所有点所走过的变动的权值之和最小是多少
条边,给出一个图中的一个生成树。在生成树上的权值是x,其他地方的权值是y,问不重复的变量完所有点所走过的变动的权值之和最小是多少
思路:
如果x>y
如果是下面情况
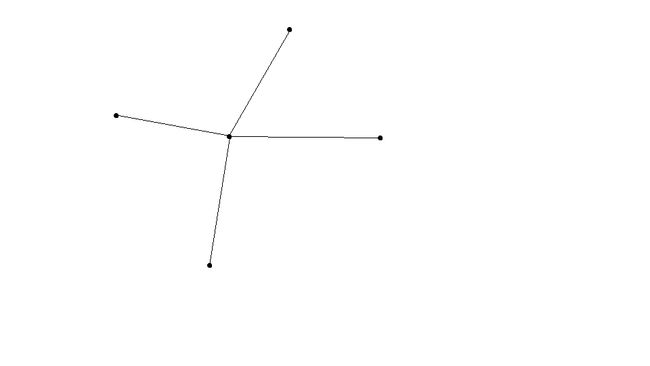
即,这棵生成树上有一个点连接了其他所有的点。这时很容易发现,存在一条路径,这个路径经过了除中间的点之外的所有的点,而且它所经过的边全都不在这棵生成树上。然后我们再把路径的终点(或起点)与中间的点相连。此时,这条路径就是经过所有点并且权值最小的一天路,此时的最小值是y*(n-2)+x;
如果不是上面的那种情况,即这棵生成树上不存在一个和其余的点都直接相连的点。此时,我们可以找到一条路,这条路经过了所有的点,而且路上的边都不在这棵生成树上,很容易证明这条路就是权值之和最小的路,此时的权值之和是y*(n-1)
如果x<y
一开始我是找树的直径,后来发现我的想法错了,例如下图
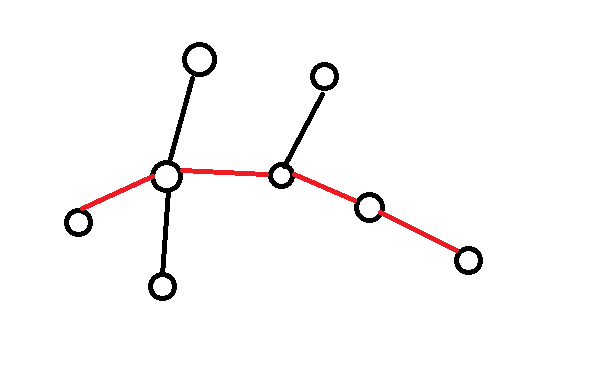
如果找树的直径的话,结果是4*x+3*y,而最优解并不是这样的,最优解如下图
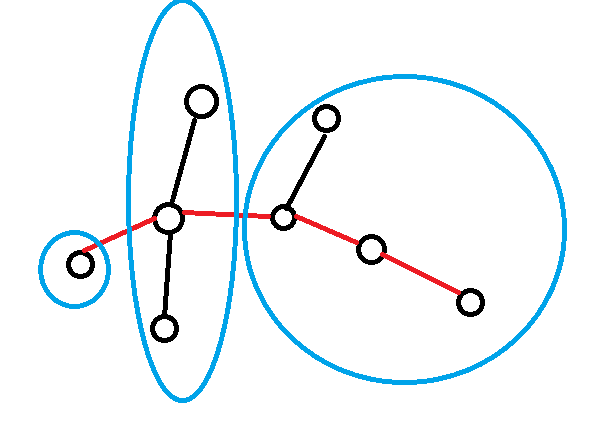
最优解是5*x+2*y (PS:以上两张图由一个学长提供)
而这道题的正确思路是将这棵树分成最少的链,由于符合题意的路径上一定有n-1条边,假如这棵树分成t条链,结果就是(t-1)*y+(n-t)*x
具体代码如下(代码和上面分析的略有不同,):
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#include <vector>
#define N 200005
#define ll long long
const int INF = 0x3fffffff;
using namespace std;
int n, r; //r为需要添加的生成树以外的边的数目
vector<int> vv[N];
int fun(int cur, int pre) //cur为当前结点, pre为上一个结点
{
int i, l = vv[cur].size(), t = 0, v;
for (i = 0; i < l; i++)
{
v = vv[cur][i];
if (v != pre) //若v == pre, 则又向前递归了
{
t += fun(v, cur);
}
}
if (cur == pre) //只有第一次的时候cur == pre, 其他递归的时候都有cur != pre
{
if (t < 3) return 0;
r += t - 2;
return 0;
}
if (t < 2) return 1;
r += t - 1; //如果这个点之后又连了多于两个边
//则需要在这里将树分开
//并且需要添加t-1条树以外的边来连接着t条链
return 0;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("1.txt", "r", stdin);
#endif
int i, j, k, u, v;
int n, x, y;
ll ans;
scanf("%d%d%d", &n, &x, &y);
for (i = 1; i < n; i++)
{
scanf("%d%d", &u, &v);
vv[u].push_back(v);
vv[v].push_back(u);
}
if (x > y)
{
ans = 1ll*y*(n-1);
for (i = 1; i <= n; i++)
if (vv[i].size() == n-1) break;
if (i <= n) ans += (ll)(x-y);
}
else if (x == y)
{
ans = 1ll*y*(n-1);
}
else
{
fun(1, 1);
ans = 1ll*r*y+1ll*x*(n-r-1);
}
printf("%I64d", ans);
return 0;
}下面的代码是看的别人的,用dp写的,但一直没弄明白,先粘上,以后dp学好了再看
#include<bits/stdc++.h>
#define N 200100
using namespace std;
vector<int> g[N];
int dp[N][2];
bool vis[N];
void DFS(int u)
{
vis[u] = true;
int m[2] = {0};
int tt = 0;
for(int i = 0;i < g[u].size();i++)
{
int v = g[u][i];
if(vis[v]) continue;
DFS(v);
if(dp[v][0] - dp[v][1] > m[0])
{
m[1] = m[0];
m[0] = dp[v][0] - dp[v][1];
}
else if(dp[v][0] - dp[v][1] > m[1])
m[1] = dp[v][0] - dp[v][1];
tt += dp[v][0];
}
dp[u][0] = tt + 1 - m[0] - m[1];
dp[u][1] = tt - m[0];
}
int main()
{
freopen("1.txt", "r", stdin);
int n, x, y, a, b;
int i;
scanf("%d%d%d", &n, &x, &y);
for(i = 1;i < n; i++)
{
scanf("%d%d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
if(x > y)
{
bool star = false;
for(i = 1; i <= n; i++)
{
if(g[i].size() == n-1)
{
star = true;
break;
}
}
if(star) printf("%I64d\n",1LL*y*(n-2)+x);
else printf("%I64d\n",1LL*y*(n-1));
}
else
{
DFS(1);
printf("%I64d\n",1LL*x*(n-dp[1][0])+1LL*y*(dp[1][0]-1));
}
return 0;
}E. Robot Arm
Roger is a robot. He has an arm that is a series of n segments connected to each other. The endpoints of the i-th segment are initially located at points (i - 1, 0) and (i, 0). The endpoint at (i - 1, 0) is colored red and the endpoint at (i, 0) is colored blue for all segments. Thus, the blue endpoint of the i-th segment is touching the red endpoint of the (i + 1)-th segment for all valid i.
Roger can move his arm in two different ways:
1. He can choose some segment and some value. This is denoted as choosing the segment number i and picking some positive l. This change happens as follows: the red endpoint of segment number i and segments from 1 to i - 1 are all fixed in place. Imagine a ray from the red endpoint to the blue endpoint. The blue endpoint and segments i + 1 through n are translated l units in the direction of this ray.

In this picture, the red point labeled A and segments before A stay in place, while the blue point labeled B and segments after B gets translated.
2. He can choose a segment and rotate it. This is denoted as choosing the segment number i, and an angle a. The red endpoint of the i-th segment will stay fixed in place. The blue endpoint of that segment and segments i + 1 to n will rotate clockwise by an angle of a degrees around the red endpoint.
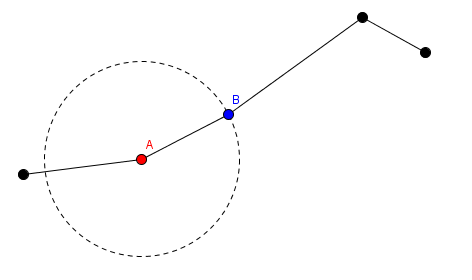

In this picture, the red point labeled A and segments before A stay in place, while the blue point labeled B and segments after B get rotated around point A.
Roger will move his arm m times. These transformations are a bit complicated, and Roger easily loses track of where the blue endpoint of the last segment is. Help him compute the coordinates of the blue endpoint of the last segment after applying each operation. Note that these operations are cumulative, and Roger’s arm may intersect itself arbitrarily during the moves.
Input
The first line of the input will contain two integers n and m (1 ≤ n, m ≤ 300 000) — the number of segments and the number of operations to perform.
Each of the next m lines contains three integers xi, yi and zi describing a move. If xi = 1, this line describes a move of type 1, where yi denotes the segment number and zi denotes the increase in the length. If xi = 2, this describes a move of type 2, where yi denotes the segment number, and zi denotes the angle in degrees. (1 ≤ xi ≤ 2, 1 ≤ yi ≤ n, 1 ≤ zi ≤ 359)
Output
Print m lines. The i-th line should contain two real values, denoting the coordinates of the blue endpoint of the last segment after applying operations 1, …, i. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 4.
Namely, let’s assume that your answer for a particular value of a coordinate is a and the answer of the jury is b. The checker program will consider your answer correct if ![]() for all coordinates.
for all coordinates.
Sample test(s)
Input
5 4
1 1 3
2 3 90
2 5 48
1 4 1
Output
8.0000000000 0.0000000000
5.0000000000 -3.0000000000
4.2568551745 -2.6691306064
4.2568551745 -3.6691306064
Note
The following pictures shows the state of the arm after each operation. The coordinates of point F are printed after applying each operation. For simplicity, we only show the blue endpoints of a segment (with the exception for the red endpoint of the first segment). For instance, the point labeled B is the blue endpoint for segment 1 and also the red endpoint for segment 2.
Initial state:
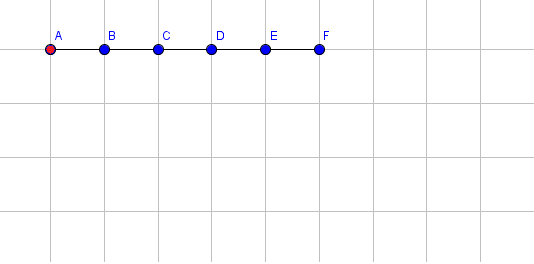
Extend segment 1 by 3.

Rotate segment 3 by 90 degrees clockwise.

Rotate segment 5 by 48 degrees clockwise.
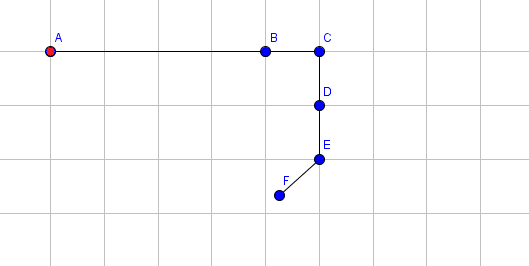
Extend segment 4 by 1.
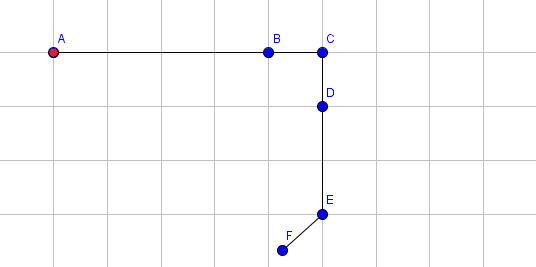
题意:
先粘上题目,明天在写 -_-#
思路:
F、G题后续会更新
