剑指offer面试题(一)
剑指offer面试题之三道经典算法:
问题一.字符替换空格，请实现一个函数，把字符数组中的每个空格替换成'%20',例如输入"we are happy.",则输出"we%20are%20happy."
拿到这样一道题目，如何去分析呢？我们通过观察替换前和替换后的字符串发现，原本空格的位置被替换成了三个字符%20,如果我们从前往后遇到空格就替换，那仫很容易导致后面的内存被覆盖，那仫如何才能解决这个问题呢？并且这个问题也存在内存分配的问题，如果面试官告诉你内存足够大，那仫你就可以尽情的使用内存啦。
最费时间的想法就是:找到空格找到后，就将空格后的字符往后移两个位置，使得%20能够不覆盖后面的字符而存储，如果遇到下一个空格后继续重复上面的步骤，但是这种想法不是高效的，我们知道它的思路是先遍历一遍字符串，找到空格后，空格后面的字符向后偏移，这使得这种算法的时间复杂度不高，为o(n^n),我们就不介绍这种算法的实现了。在这里我们提供的是另一种时间复杂度为:O(n)的算法，效率较高，搞定面试官就靠它啦！
如果我们提前知道空格的数目，并计算出替换之后的字符串长度，此时我们只需要用两个下标，一个指向旧串的最后一个字符，一个指向新开辟空间的末尾，只要遇到的不是空格，我们就将字符原模原样的赋值给新串，一旦遇到空格就倒序替换(读者可以自行画图理解，赋值是从后往前，所以是倒序替换)，这种算法是不是比上一种高效呢？下面我们就来实现以下这种算法:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void replace_black(char *str)
{
int count=0;
char *ptr=str;
int sz=strlen(str);
int newopen=0;
int oldopen=sz;
while(*ptr != '\0') //统计空格的个数
{
if(*ptr == ' ')
{
count++;
}
ptr++;
}
newopen=oldopen+2*count; //替换之后的数组的大小
while(oldopen < newopen)
{
if(str[oldopen] != ' ') //不是空格则直接将数组元素向后挪
{
str[newopen--]=str[oldopen--];
}
else //是空格则替换
{
str[newopen--]='0';
str[newopen--]='2';
str[newopen--]='%';
oldopen--;
}
}
}
int main()
{
char arr[20]="we are happy.";
replace_black(arr);
printf("替换之后的字符串是:");
printf("%s\n",arr);
system("pause");
return 0;
}
问题二.调整数组使得奇数全部位于偶数前面，题目:数组一个整形数组，实现一个函数，来调整该数组中的数字的顺序使得数组中所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分.
拿到这样一道题如何去分析呢？首先我们想到的是，如果一个数组中前半部分就是奇数，后半部分就是偶数，这当然是最好的情况啦！可是现实总是不如人意啊,如果全部的偶数都在前面而全部的奇数都位于后半部分，这当然是最糟的情况啦，此时我们对每一组数据都要交换
，当然考虑了最好和最糟的情况，接下来当然就是处于中间的情况啦！如果部分奇数在前面而部分偶数在后半部分，此时我们只需要设置两个下标，一个从前往后找第一个出现的偶数，一个从后往前找第一个出现的奇数，找到后，如果两个下标没有交叉或者没有相等就交换对应的数组元素的值，下面我们就来实现这种思路:
void sort_oddnum_evennum(int arr[],int sz)
{
int i=0;
int j=0;
int tmp=0;
for(i=0,j=sz-1;i<j;)
{
if(arr[i]%2 == 0 && arr[j]%2 == 1) //偶数在前，奇数在后，交换
{
tmp=arr[i];
arr[i]=arr[j];
arr[j]=tmp;
}
if(arr[i]%2 == 1) //奇数在前则继续向后查找
{
i++;
}
if(arr[j]%2 == 0) //偶数在后则继续向前查找
{
j--;
}
}
}
int main()
{
int sz=0;
int i=0;
int arr[10]={0};
sz=sizeof(arr)/sizeof(arr[0]);
printf("请输入你要排序的数组元素:");
for(i=0;i<sz;i++)
{
scanf("%d",&arr[i]);
}
sort_oddnum_evennum(arr,sz);
printf("排序后的结果为:");
for(i=0;i<sz;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
system("pause");
return 0;
}
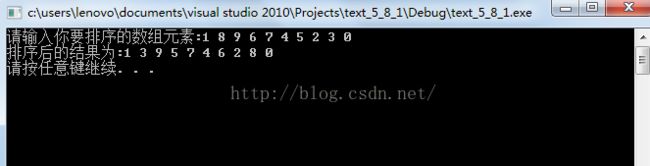
此时我们注意看它的验证结果，虽然在这个数组中奇数位与前半部分，偶数位于后半部分但是我们并没有对奇数或者偶数进行排序，它的排列是乱序的，不信请看如下结果:
问题三.有一个二维数组，数组的每行从左到右是递增的，每列从上到下是递增的，在这样的数组中查找一个数字是否存在，时间复杂度为O(n)
拿到这样一道题，最霸道的方法就是遍历整个二维数组找到就返回，当然我们需要设置两个变量，一个控制行，一个控制列，但是这种解题方法并不高效，也没有用到题目中所给出的数组的特点。下面我们就从这个数组的左上角，右上角，左下角，右下角是个角度去分析它，找到最高效的角度。
左上角:如果要找的元素比它大，由数组的特点每行从左往右是递增的，每列从上到下是递增的，我们就知道此时我们可以在第一个左上角的元素中，它的每一行的后半部分和每一列的下半部分都存在比它大的数据，那仫到底该从哪里找呢？所以这种角度舍弃掉。
左下角:如果要找的数据比它小，我们知道每一列的数据是递增的，我们可以在对应数据的前方继续寻找，如果比它大，我们只需要在最后一行中继续查找数据就可以了。这种方法似乎可以那仫是不是还有更好的角度呢？下面我们继续分析.
右上角:由数组的特点可知，右上角的元素是这一行里最大的元素，是这一列的最小元素，如果我们要查找的元素比它小，我们可以直接在这一行里继续查找，如果比右上角的元素大，那仫我们就不关心这一行了直接在下一行的右上角继续判断。这种方法似乎也可以。如果是右下角呢？下面我们来看一组数据从右上角查找的例子来帮助理解。
右下角:我们由数组的特点可知，右下角的元素是整个数组中最大的元素，如果我们要查找的元素比它小，我们知道在右下角对应的一行和一列中都比它小，那仫到底又该去哪里查找呢？所以这种角度也舍弃掉。
通过以上分析，我们找到两种角度，从右上角和左下角都可以，下面我们就来实现从右下角实现找数据的思路，我用的是递归的方法：
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
int seek_num(int arr[][4],int num,int x,int y)
{
if((x >= 0 && x<4)&& (y >= 0 && y<4))
{
if(arr[x][y] == num) //正确查找数据
return 1;
else
if(arr[x][y] < num)
return seek_num(arr,num,x+1,y);
else
return seek_num(arr,num,x,y-1);
}
return 0;
}
/* 1 2 3 4
5 8 11 14
6 9 12 15
7 10 13 16*/
int main()
{
int num=0;
int ret=0;
int arr[][4]={{1,2,3,4},{5,8,11,14},{6,9,12,15},{7,10,13,16}};
printf("请输入一个你要查找的数据:");
scanf("%d",&num);
ret=seek_num(arr,num,0,3); //从右上方开始查找
if(ret == 1)
{
printf("查找成功\n");
}
else
{
printf("查找失败\n");
}
system("pause");
return 0;
}