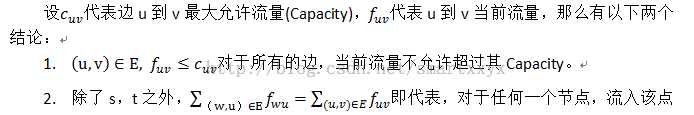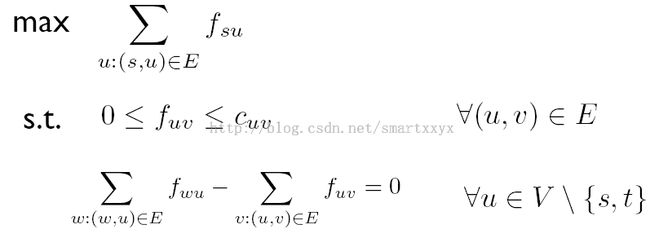图的匹配问题与最大流问题(一)

从今天开始，准备写个系列，关于图的匹配，最大流，线性规划等这些图论中的重要而且有着千丝万缕连续的问题，顺便介绍求图的最大匹配问题的著名的匈牙利算法。算是对前段时间学习的一个小结吧。Ps：本人自认很水，多多见谅。（对内容进行了部分修改，原来使用Word编辑的公式这里无法显示，只能截图了）

首先这次就先从基本的概念介绍起，顺便说说这之间的一些联系，接下来再开始一一上算法。

一、图的匹配问题

我们日常中听过最多的图的匹配问题可能就是著名的结婚问题: 在一个集合中，有m个女生，s个男生，其中1<=r<=s，设集合S1, S2, …,Si,.. ,Sm 分别代表第i个女生喜欢的男生的集合（当然一个女生可以喜欢多个男生），问有没有可能最终令这m个女生都能够和自己心仪的男生结婚？

         这个问题我们最直观的想法是，首先必须保证，任意r(<=m)个女生喜欢的男生数量必须大于等于r。这是很直观的，比如3个女生如果同时只喜欢上2个男生，则无论如何也无法分配。

而正是这一直观的想法，解决了这一问题。从上面可知，最终能够令m个女生都能和自己心仪的男生结婚的必要条件就是任意r个女生喜欢的男生的数量必须大于等于r。而通过证明，我们知道这一条件也是充分的。这一证明并不是本文的重点，所以这里略过，有兴趣，可以继续讨论。

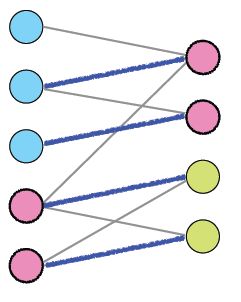
这一问题就是图的最大匹配问题。不过更一般的我们常说的图的最大匹配问题是这样描述的：对于一个二部图，其最大匹配是多少？如图，所示，最大匹配为4.

 

二、最大流问题

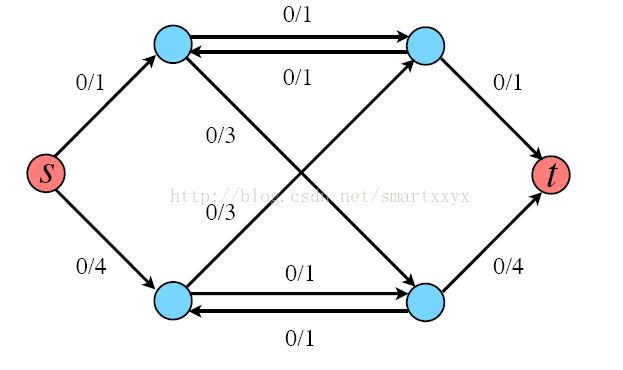
最大流问题是一个很经典的问题，很多人对此也很熟悉，它能够等同于一个线性规划问题。下面给出最大流问题的一个基本描述：如下图所示，s是源点，t为汇点，每条边上数字的含义是边能够允许流过的最大流量。可以将边看成管道，0/3代表该管道每秒最多能通过3个单位的流量，0代表当前流量。最大流问题即是说，从s点到t点，最大允许流量是多少？

那它跟线性规划又是如何产生联系的呢？这里我们先简要介绍下。

的流量等于流出该点的流量。这个可以理解为流量守恒，就如同电流一样，流入一个电阻的电流必然等于流出的电流。

那么最大流就可以表示为：

三、联系

1.      最大流等于最大二分匹配

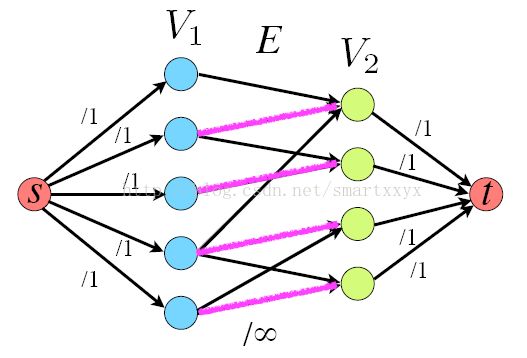
如图所示，对于一个二分图，令已有的边的容量（Capacity）为无穷大，增加一个源点s和一个汇点t，令s和t分别连接二部图中的一个分步，并设置其容量为1。这时，计算得到的最大流就等于最大二分匹配。这里的证明也会比较复杂，需要用到最大流等于最小割定理，我们以后再详细说。

2.      匈牙利算法

用最大流问题的复杂度为O（VE*E），而匈牙利算法是专门用来解决图的最大匹配问题的算法，其复杂度可以达到O（VE）。其中V代表点的数量，E代表边的数量。这是一种充分挖掘了最大匹配问题内在规律后的得到的算法，非常聪明。

3.      线性规划

上面说到了，求最大流问题可以转换为线性规划问题。而线性规划问题最著名的解法自然就是单纯形法。这种算法非常奇特，其复杂度为在最坏情况下是指数级的，但其在实践中绝大多数的情况下表现出的效率非常令人满意。而后来提出的能够在多项式时间解决线性规划问题的算法实践中表现反而没有单纯形法好。而正因为这，后来有人提出了著名的算法的平滑分析法。

4.      最大流问题其他妙用

最大流问题除了能够解决最大匹配问题外，还有其他的许多妙用。这里我们会介绍的是用最大流来解决图的点连通度和边连通度问题。点连通度是指对于一个连通图，最少删去多少点才能够使其变为非连通图。边连通度是指对于一个连通图，最少删去多少条边才能够使其变为非连通图。