uva 825 Walking on the Safe Side 走安全路线
原题:
Walking on the Safe Side
Square City is a very easy place for people to walk around. The two-way streets run North-South or East-West dividing the city into regular blocks. Most street intersections are safe for pedestrians to cross. In some of them, however, crossing is not safe and pedestrians are forced to use the available underground passages. Such intersections are avoided by walkers. The entry to the city park is on the North-West corner of town, whereas the railway station is on the South-East corner.
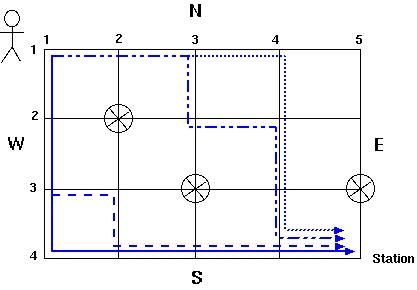
Suppose you want to go from the park to the railway station, and do not want to walk more than the required number of blocks. You also want to make your way avoiding the underground passages, that would introduce extra delay. Your task is to determine the number of different paths that you can follow from the park to the station, satisfying both requirements.
The example in the picture illustrates a city with 4 E-W streets and 5 N-S streets. Three intersections are marked as unsafe. The path from the park to the station is 3 + 4 = 7 blocks long and there are 4 such paths that avoid the underground passages.
Input
The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.
The first line of the input contains the number of East-West streets W and the number of North-South streets N. Each one of the following W lines starts with the number of an East-West street, followed by zero or more numbers of the North-South crossings which are unsafe. Streets are numbered from 1.
Output
For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.
The number of different minimal paths from the park to the station avoiding underground passages.
Sample Input
1
4 5
1
2 2
3 3 5
4
Sample Output
4
Cristina Ribeiro, MIUP’2001
题目大意:
类似高中那道经典的排列组合题目,给你一个二维坐标系。问你从(0,0)到(m,n)有多少种走法。不过这里有的点告诉你不能到达。
思路和吐槽见代码下方
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<cstring>
#include<string>
#include<cmath>
#include <iomanip>
using namespace std;
int dp[500][500];
bool Map[500][500];
int main()
{
// ios::sync_with_stdio(false);
int t,r,c,q;
char ch[1000];
scanf("%d",&t);
getchar();
while(t--)
{
scanf("%d%d",&r,&c);getchar();
memset(dp,0,sizeof(dp));
memset(Map,false,sizeof(Map));
for(int i=1;i<=r;i++)
{
scanf("%d",&q);
gets(ch);
int len=strlen(ch);
int index=0;
for(int j=0;j<=len;j++)
{
if(ch[j]-'0'>=0&&ch[j]-'0'<=9)
{
index=index*10+ch[j]-'0';
}
else
{
Map[q][index]=1;
index=0;
}
}
}
dp[1][0]=1;
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
if(!Map[i][j])
dp[i][j]=dp[i-1][j]+dp[i][j-1];
printf("%d\n",dp[r][c]);
if(t)
printf("\n");
}
return 0;
}
思路:
此题很简单,难点在于输入输出,此题我交了能有10次,就是不对,但是感觉思路没问题啊~去别人博客上看,发现别人也是这么做的。。我把别人输入数据的代码偷过来然后就过了
思路dp[i]=dp[i-1][j]+dp[i][j-1](如果(i,j)可达,否则dp[i][j]=0)