算法导论12.2-8 从任意结点使用后继函数k次的时间复杂度为O(k+h)
从任意结点使用后继函数k次,假设二叉搜索树的高度为h,则时间复杂度为O(k+h)
分析
从表面上来看,回溯父结点的复杂度为O(h),如果多次回溯,则总体复杂度可能远超O(k+h)
再想使用数学归纳法,假设起始结点和回溯结点分别位于某个结点的左右子树,然后发现无法使用替换法证明。最后从12.2-7 中得到一丝信息,即只要证明后继函数k次后,访问结点的总次数为O(k+h)即可
证明
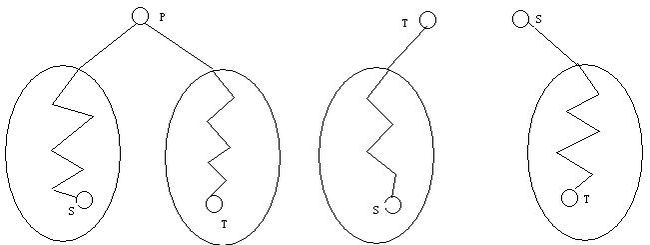
设定遍历的起始结点为S,结束结点为T,则S和T的关系总共有3种(如下图)。
(1) S 和 T有共同的祖先结点p,S在P的左子树,T在P的右子树
(2) T 为S的祖先,S在T的左子树中
(3) S 为T的祖先,T在S的右子树中
下面仅证明在(1) 的情形,(2) (3)可类似证明在(1) 的情形下,设S到P的折线段为Ls,T到P的折线段为Lt,
先证明一个简单的引理,从S访问到P,仅仅访问Ls右方、Lt左方的结点,这个引理看起来也是对的,假设Ls上某个结点x的左孩子y,则S存在于结点x的右子树,从bst_successor 代码可以发现,回溯时仅仅访问父结点,不会访问到父结点的左孩子,只可能访问父结点的右孩子,所以y结点不可能访问到
再证明一个简单的引理,在(1) 的情形下,P的左子树中所有在Ls右方的所有结点都会作为后继被遍历到
假设Ls上某个结点x,有右子树y,则S在结点x的左子树上,所以有 S< x < y < P,所以结点x的右子树的所有结点都会作为后继被遍历到
假设S=>T的遍历过程,在P左子树遍历r个结点,在P右子树遍历s个结点,则k = r + s + 2,2是因为要访问到P和P的右子树的最小结点。再证明P左子树访问结点个数最多为 r + (h-1),因为除了Ls上的结点,P左子树在Ls右方的所有结点都是后继,都在r中,最多是Ls上的结点不属于后续结点,Ls长度最长为h-1
根据12.2-7的证明,P左子树访问结点总次数 H(r, h-1) <= 2(r+h-1),P右子树访问结点总次数 H(s, h-1) <= 2(s+h-1),S=>T遍历过程访问结点次数
H(k,h) <= H(r, h-1) + (h-1) + 1 + (h-1) + 1 + H(s,h-1)
H(k,h) <= 2(r+h-1) + (h-1) + 1 + (h-1) + 1 + 2(s+h-1)=2(k+2h-2)=O(k+h)
当S和T有子结点时也很好证明,(2) (3)情形也可以类似证明