GBDT（Gradient boosting decision tree）算法

GBDT 又称MART（Multiple Additive Regression Tree），“是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力（generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。”

GBDT可用于所有（线性/非线性）回归问题（LR只能用于线性问题）

基本概念

1. DT --> 回归树

树一般分为 回归树 和 分类树

回归树用于预测实数值，其结果加减有意义
                分类树用于分类，其结果不能加减

GBDT为回归树，其结果是所有树的累加

2. GB --> 梯度提升

boosting方法的基本思想是，训练多个弱分类器，每个分类器是某一个方面的专家，然后通过联合所有弱分类器，组成一个强分类器

具体的联合方式有多种方案，一种是投票形式，对每个分类器设置权重，每轮迭代对分错的分类器提升其权重，分对的分类器降低其权重（adaboost）

    一种是串联形式，后一个分类器的输入取决于上一个分类器的输出（gbdt）

算法流程

图和例子来自 http://blog.csdn.net/w28971023/article/details/8240756

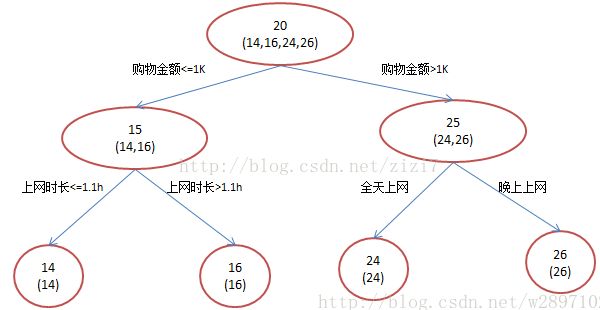
预测A、B、C、D四个人的年龄，首先使用传统的回归树训练，一个可能的分类树为

可以看到，虽然结构较为简单，但类似 1.1h、1K 的条件太严苛，很容易使模型陷入过拟合

使用GBDT的方法，一个可能的分类模型为

“由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。”

Shrinkage

该理论主要是为了防止模型因为收敛太快而陷入过拟合，仅取每棵树的一部分加入分类模型

更新公式：y(1~i) = y(1~i-1)  + step * y(i)

其中step是shrinkage，一般取0.01~0.001

实现

算法过程较为简单，但决策树的建立是个关键（http://blog.csdn.net/dark_scope/article/details/13168827）

有一个GBDT的代码简介http://blog.csdn.net/w28971023/article/details/8249108

此外opencv貌似也有实现，有时间看看

参考

[1] http://blog.csdn.net/w28971023/article/details/8240756（GBDT）

[2] http://blog.csdn.net/dark_scope/article/details/14103983（adaboost）