大端模式Big Endian和小端模式Little Endian以及浮点数在内存中的存储

大端模式和小端模式存放数据的区别很简单：大端模式先存放数据的高位字节，小端模式先存放数据的低位字节。

比如 int a=1，a所占的四个字节16进制标示：00 00 00 01。假设在内存中从100这个位置开始存放a。

大端模式存放：00 00 00 01，所占地址分别是：100 101 102 103

小端模式存放：01 00 00 00，与大端模式刚好相反。

写一个函数判断机器是不是大端模式：

bool isBigendian()
{
    int a=1;
    char *pa=(char *)&a;
    if((*pa)==0x01)
    {
        return false;
    }
    else
    {
        return true;
    }
}

x86 Intel计算机使用的是小端模式（little endian）。我们可以用上面的函数验证一下。那么问题来了，挖掘技术哪家强？中国~~~哈哈，开个玩笑。我想说的是浮点数在内存中怎么存储？

我们知道，浮点数分为单精度(float)和双精度（double)两种。float类型占4byte内存，double类型占8byte内存。浮点数的二进制存储标准遵循IEEE 754标准。下面定义一个浮点数，然后输出它每个字节内容。

void showbytes(unsigned char *p,int len) // 注意这个p指针类型必须是unsigned char，后边才能表示出真实的字节内容。要不然会进行符号位扩展。
{
    for(int i=0;i<len;i++)
    {
        printf("%x ",*(p++));
    }
    printf("\n");
}

int main()
{
    if(isBigending())
    {
        cout<<"this system is big endian"<<endl;
    }
    else
    {
        cout<<"this system is  little endian"<<endl;
    }

    float f=1.1;
    double d1=1.1;
    double d2=f;// f类型提升
    cout<<"f store as :"<<endl;
    showbytes((unsigned char *)&f,sizeof(f));
    cout<<"d1 store as :"<<endl;
    showbytes((unsigned char *)&d1,sizeof(d1));
    cout<<"d2 store as :"<<endl;
    showbytes((unsigned char *)&d2,sizeof(d2));

}

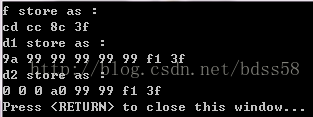
运行结果：

由于是小端模式，所以f存储到内存里后内存里内容为3f 8c cc cd 二进制：0011 1111 1000 1100 1100 1100 1100 1101

同理，d1在内存里的内容为3f f1 99 99 99 99 99 a9 二进制：0011 1111 1111 0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 1001

同理，d2在内存中的内容为3f f1 99 99 a0 00 00 00二进制：0011 1111 1111 0001 1001 1001 1001 1001 1010 0000 0000 0000 0000 0000 0000 0000

IEEE754标准规定单精度浮点数：1位符号位，8位阶码，23位尾数。那么f的：

符号位：0

阶码：01111111，十进制阶码就是0

尾数：000 1100 1100 1100 1100 1101

转换成十进制约为1.1

IEEE754标准规定双精度浮点数：1位符号位，11位阶码，52位尾数。那么d1的：

符号位：0

阶码：011 1111 1111，十进制阶码就是0

尾数：0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 1001

转换成十进制约为1.1

那么d2的：

符号位：0

阶码：011 1111 1111，十进制阶码就是0

尾数：0001 1001 1001 1001 1001 1010 0000 0000 0000 0000 0000 0000 0000

转换成十进制约为1.1

可以发现，d2的尾数就是f的尾数。f类型提升后低位填充0，所以精度并没有提高。