插值
拉格朗日插值法
由此容易写出程序
#include <stdio.h>
int main()
{
int i,j,n;
double x[100],y[100];
double temp,m,result;
printf("请输入已知点的对数\n");
scanf("%d",&n);
printf("请输入点的横坐标与纵坐标\n");
for (i=0;i<n;i++)
scanf("%lf%lf",&x[i],&y[i]);
printf("请输入插值点的横坐标\n");
scanf("%lf",&m);
result=0;
for (i=0;i<n;i++)
{
temp=y[i];
for (j=0;j<n;j++)
{
if (i!=j)
{
temp=temp*(m-x[j]);
temp=temp/(x[i]-x[j]);
}
}
result=result+temp;
}
printf("%.4f\n",result);
return 0;
}
拉格朗日插值法是当待求的系数是多项式时(而不是三角函数之类的时)可以采用的一种方法。
用于:已知多个点的横纵坐标,告知一个新横坐标,在满足新的曲线经过所有的点的要求下,所求得的纵坐标。
下面介绍matlab的差值函数:
interp1(x0,y0,x,'method')
method为插值方法,所有的插值方法要求x0是单调的
比如
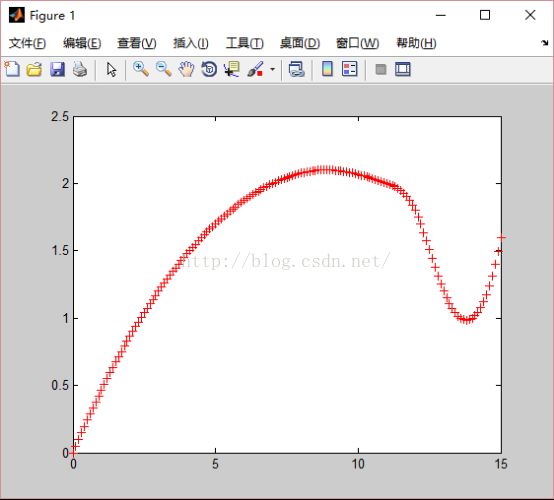
<pre name="code" class="objc">>> x0=[0 3 5 7 9 11 12 13 14 15]; >> y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];>> y1=interp1(x0,y0,x)
>> plot(x,y1,'r+')

由于没有指定参数,默认为线性插值,可以看出图形是有些生硬的。
这里引入三次样条插值:
>> x0=[0 3 5 7 9 11 12 13 14 15]; >> y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6]; >>pp1=csape(x0,y0) >>y3=fnval(pp1,x) >>plot(x,y3,'r+')这里csape默认返回的是pp形式,也就是多项式格式
所以必须跟上fnval
明显好转,尤其是后面部分。
通过这个方法可以求得插入的纵坐标的值,那么怎么知道表达式的值,也就是多项式的系数呢
pp1.coefs
ans =
0.0007 -0.0356 0.5007 0
0.0009 -0.0295 0.3054 1.2000
0.0001 -0.0242 0.1981 1.7000
-0.0012 -0.0237 0.1023 2.0000
0.0048 -0.0310 -0.0072 2.1000
-0.1241 -0.0022 -0.0736 2.0000
0.2252 -0.3747 -0.4505 1.8000
0.0234 0.3009 -0.5243 1.2000
0.0811 0.3712 0.1477 1.0000
也就是0.007(t-0)^3-0.0356(t-3)^2+0.5007*(t-5)+0=0 (t属于[0,1.2))
....
.....
例5.2:
>> x0=[0.15 0.16 0.17 0.18]; >> x1=[3.5 1.5 2.5 2.8]; >> pp=csape(x0,x1) >> format long g >> s=quadl(@(t)ppval(pp,t),0.15,0.18) >> format%恢复精度
姜启源10.1牙膏的销售量
假设y=b0+b1x1+b2x2+b3x2^2
>> x1=[-0.05 0.25 0.6 0 0.25 0.20 0.15 0.05 -0.15 0.15 0.20 0.10]; >> x2=[5.50 6.75 7.25 5.50 7.00 6.50 6.75 5.25 5.25 6.00 6.50 6.25]; >> x3=x2.*x2; >> y=[7.38 8.51 9.52 7.50 9.33 8.28 8.75 7.87 7.10 8.00 7.89 8.15]; >> t=[ones(size(x1,2),1),x1',x2',x3']; >> [b,bint,r,rint,stats]=regress(y',t)
b =
20.1175
0.6718
-4.7850
0.4535
bint =
-0.8306 41.0657
-1.6821 3.0258
-11.8268 2.2568
-0.1376 1.0445
r =
-0.1045
-0.1389
-0.1459
-0.0181
0.3185
-0.0293
0.1683
0.3408
-0.2948
0.1661
-0.4193
0.1571
rint =
-0.7131 0.5040
-0.7578 0.4801
-0.3889 0.0971
-0.6348 0.5986
-0.1240 0.7610
-0.6463 0.5876
-0.3786 0.7152
-0.0708 0.7525
-0.6816 0.0920
-0.3626 0.6947
-0.9170 0.0784
-0.4334 0.7476
stats =
0.8985 23.5939 0.0003 0.0767
stats的第一个参数越接近1越好,第三个参数越接近0越好,而rint是置信区间,一般不包含0点
修改模型为
y=b0+b1+b2x2+b3x3^2+b4x1*x2
>> x4=x1.*x2; >> t=[ones(size(x1,2),1),x1',x2',x3',x4']; >> [b,bint,r,rint,stats]=regress(y',t)
b =
45.3460
16.3022
-13.2507
1.1584
-2.4088
bint =
17.3825 73.3095
2.1064 30.4980
-22.6398 -3.8616
0.3745 1.9423
-4.5783 -0.2394
r =
0.0241
-0.1837
0.0506
-0.0085
0.1175
-0.0075
0.0605
-0.0208
-0.0597
0.1786
-0.3975
0.2464
rint =
-0.4426 0.4908
-0.6447 0.2772
-0.0365 0.1376
-0.4934 0.4763
-0.2253 0.4604
-0.4925 0.4774
-0.3681 0.4892
-0.2082 0.1665
-0.3383 0.2190
-0.2160 0.5733
-0.6941 -0.1010
-0.1572 0.6501
stats =
0.9488 32.4545 0.0001 0.0442
明显看出效果提高。