重温数据结构：平衡二叉树（AVL树）、红黑树、TreeSet与TreeMap

写作目的：

本博客的目的是认识和复习数据结构中的平衡二叉树和红黑树，以及由红黑树实现的TreeSet和TreeMap

1.二叉搜索树的弊端

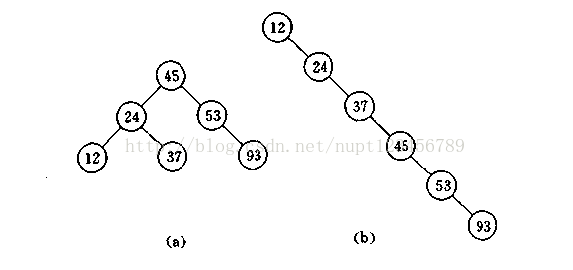
二叉搜索树的查找,插入,删除的复杂度等于树的高度，时间复杂度是O(log(n)).但是，对于同一组数据，插入顺序的不同，可能会导致二叉搜索树的高度不同。如果是有序插入，二叉搜索树退化成链表，其查找的时间复杂度退化为O(n).

图 插入顺序不同对二叉搜索树的影响

2.平衡二叉树（AVL树）

[维基百科]：在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis。

平衡二叉树的递归定义：

平衡二叉树或为空树,或为如下性质的二叉排序树:

（1）左右子树深度之差的绝对值不超过1;

（2）左右子树仍然为平衡二叉树.

 其中，平衡因子BF=左子树深度－右子树深度.

平衡二叉树每个结点的平衡因子只能是1，0，-1。若其绝对值超过1，则该二叉排序树就是不平衡的。

3.AVL树的插入操作

1).若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。首先要找出插入新结点后失去平衡的最小子树根结点的指针。然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。

2).当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。

 失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。

举例：

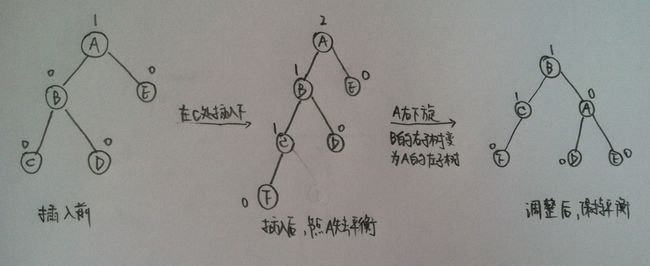
A)LL型（左孩子的左子树）

由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行一次顺时针旋转操作。 即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。而原来B的右子树则变成A的左子树。

B）RR型平衡旋转法(右孩子的右子树)

由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行一次逆时针旋转操作。即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。而原来C的左子树则变成A的右子树。

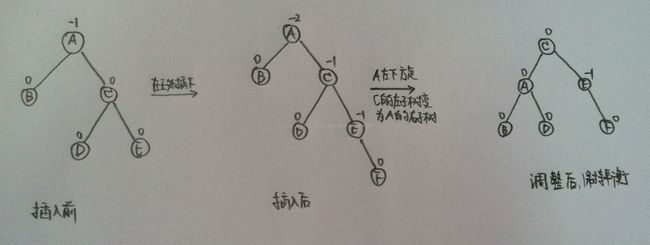
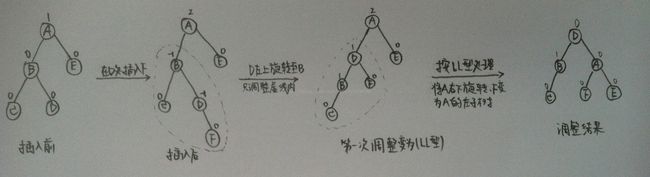
C)LR型平衡旋转法（左孩子的右子树）

由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行两次旋转操作（先逆时针，后顺时针）。即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。即先使之成为LL型，再按LL型处理。

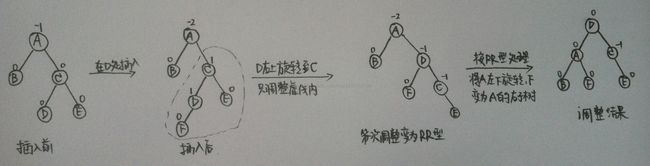
D)RL型平衡旋转法  

由于在A的右孩子C的左子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行两次旋转操作（先顺时针，后逆时针），即先将A结点的右孩子C的左子树的根结点D向右上旋转提升到C结点的位置，然后再把该D结点向左上旋转提升到A结点的位置。即先使之成为RR型，再按RR型处理。

4.红黑树

红黑树并不追求“完全平衡”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。红黑树能够以O(log n) 的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。当然，还有一些更好的，但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡，但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同，但统计性能比AVL树更高。

红黑树的定义：

一颗二叉查找树如果满足下面的红黑性质，则为一颗红黑树：

1.每个节点或者是红，或者是黑

2.根节点是黑的

3.每个叶子节点是黑色的

4.如果一个节点是红色的，则它的两个孩子都是黑的

5.每个节点，从该节点到其子孙节点的所有路径上包含相同数目的黑节点

红黑树的典型应用是“关联数组”.红黑树的Java实现参见参考博客。

5.Java中的TreeSet与TreeMap

Java中的TreeMap和TreeSet是由红黑树实现的。这两个容器除了要求里面的元素不能重复之外，还要求元素实现了Comparable接口。即按照Comparable对元素进行排序。由于TreeMap是由红黑树实现,所以一般查找时间复杂度为 o(lg(n)),这个效率当然没有HashMap的效率高.不过TreeMap比HashMap功能强大,如果不需要排序的话当然不会用TreeMap,如果需要排序的话,HashMap无法胜任,当然要用TreeMap了。另外还有一个LinkedHashMap，LinkedHashMap 是HashMap的一个子类，保存了记录的插入顺序，在用Iterator遍历LinkedHashMap时，先得到的记录肯定是先插入的.

参考博客：

【1】http://blog.csdn.net/do2jiang/article/details/5529770

【2】维基百科：http://zh.wikipedia.org/wiki/AVL%E6%A0%91

【3】红黑树的java实现:http://blog.csdn.net/yaoweijq/article/details/5833770

【4】红黑树的Java实现：http://justsee.iteye.com/blog/1107310