Fast HOG源码注释

DPM中使用的HOG特征提取方法，和原始的HOG不太一样，比原来的要快一些，检测效果也好一些。下边的代码是从作者的目标检测中抽出的，详情见这里。虽然已经比原始HOG快了不少，但仍有一些优化空间，比如代码中存在一些不必要的乘法，多余的计算等。

//fast hog 源码注释，求出的特征和原始的特征不太一样
//参考论文“Object detection with discriminatively train part based models”
//[email protected]


#include <math.h>
#include "mex.h"

// small value, used to avoid division by zero
#define eps 0.0001

// unit vectors used to compute gradient orientation
//把cos(a)和sin(a)按[0, pi]分为9个bin，快速近似计算梯度方向使用
double uu[9] = {1.0000, 
		0.9397, 
		0.7660, 
		0.500, 
		0.1736, 
		-0.1736, 
		-0.5000, 
		-0.7660, 
		-0.9397};
double vv[9] = {0.0000, 
		0.3420, 
		0.6428, 
		0.8660, 
		0.9848, 
		0.9848, 
		0.8660, 
		0.6428, 
		0.3420};

static inline float min(float x, float y) { return (x <= y ? x : y); }
static inline float max(float x, float y) { return (x <= y ? y : x); }

static inline int min(int x, int y) { return (x <= y ? x : y); }
static inline int max(int x, int y) { return (x <= y ? y : x); }

// main function:
// takes a double color image and a bin size 
// returns HOG features
//输入：三通道图像，每个cell的大小8x8
mxArray *process(const mxArray *mximage, const mxArray *mxsbin) {
  double *im = (double *)mxGetPr(mximage);
  const int *dims = mxGetDimensions(mximage);//图像维度三个值分别是{H, W, C}；
  if (mxGetNumberOfDimensions(mximage) != 3 ||
      dims[2] != 3 ||
      mxGetClassID(mximage) != mxDOUBLE_CLASS)
    mexErrMsgTxt("Invalid input");

  int sbin = (int)mxGetScalar(mxsbin);

  // memory for caching orientation histograms & their norms
  int blocks[2];//这里用block来表示一个8x8的小块，paper里是用cell来表示，表搞混了，这个数组存的是H和W各可以划分多少cell
  blocks[0] = (int)round((double)dims[0]/(double)sbin);//H方向多少个cell
  blocks[1] = (int)round((double)dims[1]/(double)sbin);//W方向多少个cell
  float *hist = (float *)mxCalloc(blocks[0]*blocks[1]*18, sizeof(float));//存梯度的直方图，每个方向一页，总共18个方向，共18页
  float *norm = (float *)mxCalloc(blocks[0]*blocks[1], sizeof(float));//归一化因子，

  // memory for HOG features
  int out[3];//输出特征的维数
  out[0] = max(blocks[0]-2, 0);//减2的原因：因为图像没有扩展，直方图的第一行，第一列和最后一行，最后一列不方便计算，所以宽、高各减去一
  out[1] = max(blocks[1]-2, 0);
  out[2] = 27+4+1;//每个cell的最终输出维度为32维，不同于原始HOG的36维
  mxArray *mxfeat = mxCreateNumericArray(3, out, mxSINGLE_CLASS, mxREAL);//分配输出内存空间
  float *feat = (float *)mxGetPr(mxfeat);
  
  int visible[2];//输入图像不一定是cell大小的整数倍，因此要进行裁剪，这里存的是裁剪后的H,W；
  visible[0] = blocks[0]*sbin;
  visible[1] = blocks[1]*sbin;
  
  //这个循环计算梯度方向和幅值，并投影到相应的梯度直方图中
  for (int x = 1; x < visible[1]-1; x++) {
    for (int y = 1; y < visible[0]-1; y++) {
	  //下边计算三个通道的x,y方向梯度，取幅值最大的幅值、dx、dy作为有效值
      // first color channel
      double *s = im + min(x, dims[1]-2)*dims[0] + min(y, dims[0]-2);
      double dy = *(s+1) - *(s-1);
      double dx = *(s+dims[0]) - *(s-dims[0]);
      double v = dx*dx + dy*dy;

      // second color channel
      s += dims[0]*dims[1];
      double dy2 = *(s+1) - *(s-1);
      double dx2 = *(s+dims[0]) - *(s-dims[0]);
      double v2 = dx2*dx2 + dy2*dy2;

      // third color channel
      s += dims[0]*dims[1];
      double dy3 = *(s+1) - *(s-1);
      double dx3 = *(s+dims[0]) - *(s-dims[0]);
      double v3 = dx3*dx3 + dy3*dy3;

      // pick channel with strongest gradient
      if (v2 > v) {
        v = v2;
        dx = dx2;
        dy = dy2;
      } 
      if (v3 > v) {
        v = v3;
        dx = dx3;
        dy = dy3;
      }

	  //找到当前的梯度应该投影到那个bin，[0, 2xPI]总共18个bin
	  //最后写这里是如何找到最合适的bin,这是快速近似算法
      // snap to one of 18 orientations
      double best_dot = 0;
      int best_o = 0;
      for (int o = 0; o < 9; o++) {
        double dot = uu[o]*dx + vv[o]*dy;
        if (dot > best_dot) {
          best_dot = dot;
          best_o = o;
        } else if (-dot > best_dot) {
          best_dot = -dot;
          best_o = o+9;
        }
      } 
      
	  //下边这几行代码就是用来线性插值的，注意这里没有使用三线性插值和原始HOG不一样
	  //省略了梯度的插值
      // add to 4 histograms around pixel using linear interpolation
      double xp = ((double)x+0.5)/(double)sbin - 0.5;
      double yp = ((double)y+0.5)/(double)sbin - 0.5;
      int ixp = (int)floor(xp);
      int iyp = (int)floor(yp);
      double vx0 = xp-ixp;
      double vy0 = yp-iyp;
      double vx1 = 1.0-vx0;
      double vy1 = 1.0-vy0;
      v = sqrt(v);

	  //当前像素对左下角cell有贡献
	  //hist + ixp*blocks[0] + iyp -- 右下角cell的位置
	  //blocks[0]*blocks[1] -- 一页大小
	  //best_o*blocks[0]*blocks[1] -- 最合适的梯度坐在页 
      if (ixp >= 0 && iyp >= 0) {
        *(hist + ixp*blocks[0] + iyp + best_o*blocks[0]*blocks[1]) += 
          vx1*vy1*v;
      }

	  //当前像素对下方cell有贡献
      if (ixp+1 < blocks[1] && iyp >= 0) {
        *(hist + (ixp+1)*blocks[0] + iyp + best_o*blocks[0]*blocks[1]) += 
          vx0*vy1*v;
      }
	  //当前像素对左边cell有贡献
      if (ixp >= 0 && iyp+1 < blocks[0]) {
        *(hist + ixp*blocks[0] + (iyp+1) + best_o*blocks[0]*blocks[1]) += 
          vx1*vy0*v;
      }
	  //当前像素对所在cell有贡献
      if (ixp+1 < blocks[1] && iyp+1 < blocks[0]) {
        *(hist + (ixp+1)*blocks[0] + (iyp+1) + best_o*blocks[0]*blocks[1]) += 
          vx0*vy0*v;
      }
	  //关于这一点之前的HOG特征分析中有，只不过这里是直接对附近的cell贡献，原始的HOG是对Block，原理是一样的根据空间距离插值
    }
  }

  // compute energy in each block by summing over orientations
  // energy 不晓得应该怎么翻译，这里是计算归一化因子的
  // 因为上边是把[0， 2PI]分为18个方向，举个例子10度和190度算作两个方向
  // 这里归一化的时候要把10度和190度两个方向算作一个方向，因此要加在一起然后求平方
  // norm是blocks[0]*blocks[1]大小的，每一个位置存的是所有梯度方向的平方和
  for (int o = 0; o < 9; o++) {
    float *src1 = hist + o*blocks[0]*blocks[1];
    float *src2 = hist + (o+9)*blocks[0]*blocks[1];
    float *dst = norm;
    float *end = norm + blocks[1]*blocks[0];
    while (dst < end) {
      *(dst++) += (*src1 + *src2) * (*src1 + *src2);
      src1++;
      src2++;
    }
  }

  // compute features
  //计算特征，out[0] = blocks[0] - 2, out[1] = blocks[1] - 2; 防止越界
  for (int x = 0; x < out[1]; x++) {
    for (int y = 0; y < out[0]; y++) {
      float *dst = feat + x*out[0] + y;      
      float *src, *p, n1, n2, n3, n4;
	  //根据上边计算出的energy求出归一化因子
	  //每个cell分属四个block（这个block是2x2个cell的那个block！表混淆）,因此要归一化四次，下边就是求四个归一化因子
      p = norm + (x+1)*blocks[0] + y+1;
      n1 = 1.0 / sqrt(*p + *(p+1) + *(p+blocks[0]) + *(p+blocks[0]+1) + eps);
      p = norm + (x+1)*blocks[0] + y;
      n2 = 1.0 / sqrt(*p + *(p+1) + *(p+blocks[0]) + *(p+blocks[0]+1) + eps);
      p = norm + x*blocks[0] + y+1;
      n3 = 1.0 / sqrt(*p + *(p+1) + *(p+blocks[0]) + *(p+blocks[0]+1) + eps);
      p = norm + x*blocks[0] + y;      
      n4 = 1.0 / sqrt(*p + *(p+1) + *(p+blocks[0]) + *(p+blocks[0]+1) + eps);

      float t1 = 0;
      float t2 = 0;
      float t3 = 0;
      float t4 = 0;

      // contrast-sensitive features
	  //这里把18个方向作为18个特征，也就是10度和190度是不同的特征
      src = hist + (x+1)*blocks[0] + (y+1);
      for (int o = 0; o < 18; o++) {
        float h1 = min(*src * n1, 0.2);//clip, 大于0.2的特征值截断
        float h2 = min(*src * n2, 0.2);
        float h3 = min(*src * n3, 0.2);
        float h4 = min(*src * n4, 0.2);
        *dst = 0.5 * (h1 + h2 + h3 + h4);//四个归一化之后的特征值求和除以2，为什么？请看论文
        t1 += h1;//当前cell所在的四个block归一化后的特征值分别加起来
        t2 += h2;
        t3 += h3;
        t4 += h4;
        dst += out[0]*out[1];
        src += blocks[0]*blocks[1];
      }

      // contrast-insensitive features
	  //这里把10度和190度算作一个特征，所以要求一个sum然后再归一化四次
      src = hist + (x+1)*blocks[0] + (y+1);
      for (int o = 0; o < 9; o++) {
        float sum = *src + *(src + 9*blocks[0]*blocks[1]);
        float h1 = min(sum * n1, 0.2);
        float h2 = min(sum * n2, 0.2);
        float h3 = min(sum * n3, 0.2);
        float h4 = min(sum * n4, 0.2);
        *dst = 0.5 * (h1 + h2 + h3 + h4);
        dst += out[0]*out[1];
        src += blocks[0]*blocks[1];
      }

      // texture features
	  //纹理特征，cell所在的四个block的特征值的和乘以一个系数？？？
      *dst = 0.2357 * t1;
      dst += out[0]*out[1];
      *dst = 0.2357 * t2;
      dst += out[0]*out[1];
      *dst = 0.2357 * t3;
      dst += out[0]*out[1];
      *dst = 0.2357 * t4;

      // truncation feature
	  //最后一个特征是0，
      dst += out[0]*out[1];
      *dst = 0;
    }
  }

  mxFree(hist);
  mxFree(norm);
  return mxfeat;
}

// matlab entry point
// F = features(image, bin)
// image should be color with double values
void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[]) { 
  if (nrhs != 2)
    mexErrMsgTxt("Wrong number of inputs"); 
  if (nlhs != 1)
    mexErrMsgTxt("Wrong number of outputs");
  plhs[0] = process(prhs[0], prhs[1]);
}

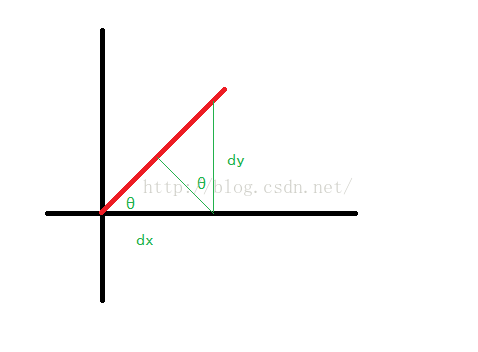
上边红线的长度可以用cos(theta)*dx + sin(theta)*dy表示

代码中从[0，pi]一个一个试找到最大的那个长度，这个角度就是最接近theta的角度

dx, dy可能小于0，长度也可能是负的，因此代码中把角度从【0，pi】扩展到【0,2pi】共18个方向

以上理解的有问题欢迎联系我 [email protected]

我前几天写的HOG特征分析怎么没了， F.U.C.K......