压缩感知中常用的待还原信号种类
研究压缩感知的一个基本工作就是生成原始的信号,也就是y=Ax中的x。一般来说,x是一个长度为N的列向量,稀疏度为k,其中x的非零位置组成的集合称作支撑集T。
x中的非零元素集合一般独立同分布四种随机分布。
1、Uniform,开区间(0,1)上的均匀分布。
2、Signs,伯努利分布,待选集合为{-1,1},等概率选取。
3、Gaussian,标准正态分布N(0,1)
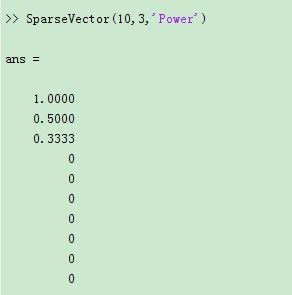
4、Power,能量法则,1/j,j=1,...,k的某个排列组合。
基于这些生成的向量,我们就可以进一步做算法研究了,比如算法重构性能的研究。
下边附上相关的Matlab程序,它摘自斯坦福大学的一个开源包,http://sparselab.stanford.edu/
路径为SparseLab2.1-Core\Utilities\
SparseVector.m
可能是因为Matlab版本的问题,我用的是8.0.0.783 (R2012b),程序有一点错误,我已经做了修改,可以参考代码中的中文注释。
附:Matlab程序——SparseVector.m
function x = SparseVector(n, k, ensemble, perm)
% SparseVector: Generates a sparse vector with a specified distribution.
%
% Usage:
% x = SparseVector(n, k, ensemble, perm)
% Inputs:
% n vector length
% k number of nonzero entries
% ensemble string containing name of coefficient distribution
% 'Uniform', 'Gaussian', 'Signs', 'Power'.
% Default is 'Uniform'.
% perm If =1, the nonzero indices are randomly selected.
% Otherwise, the nonzero entries are in indices 1..k (default).
% Outputs:
% x Sparse n vector.
% Description:
% This function creates a vector of length n with k nonzero entries,
% distributed according to the specified input ensemble.
% The following distributions are supported:
%
% 'Uniform' - Entries are distributed uniformly on the unit interval.
%
% 'Gaussian' - Entries are distributed N(0,1).
%
% 'Signs' - Entries are distributed Bernoulli over the set {-1,1},
% with equal probabilities.
%
% 'Power' - Entries follow the power law 1/j, j = 1..k
%
% See Also
% MatrixEnsemble
if nargin < 4,
perm = 0;
end
if nargin < 3,
ensemble = 'Uniform';
end
switch upper(ensemble)
case 'UNIFORM'
x = [rand(k,1); zeros(n-k,1)];
case 'SIGNS'
x = sign(rand(k,1) - 0.5);
zz = find(x == 0);
Phi(zz) = ones(size(zz));
x = [x; zeros(n-k,1)];
case 'GAUSSIAN'
x = [randn(k,1); zeros(n-k,1)];
case 'POWER'
%这里被我修改了,之前是x = [1./[1:k]; zeros(n-k,1)];
%程序是有问题的,需要转置
x = [(1./[1:k])'; zeros(n-k,1)];
end
if perm
p = randperm(n);
x = x(p);
end
%
% Copyright (c) 2006. David Donoho
%
%
% Part of SparseLab Version:100
% Created Tuesday March 28, 2006
% This is Copyrighted Material
% For Copying permissions see COPYING.m
% Comments? e-mail sparselab@stanford.edu
%
接下文《压缩感知中常用的观测矩阵》 http://blog.csdn.net/zhyoulun/article/details/25604293