trie tree

trie tree也叫字典树，快速的解决类似对于每一个给出的字符串，如何在词典（一组字符串）里面找到以这个字符串开头的所有单词这样的问题。

对于少量的查询，当然可以对每个需要查询的字符串，依次遍历词典里的所有单词，检查需要查询的字符串是不是这个单词的前缀就行了。可是对于大量数据的运行效果就会指数级的变差。用一棵树来表示整个词典就能很好的解决这个问题。这样的数就是trie tree。

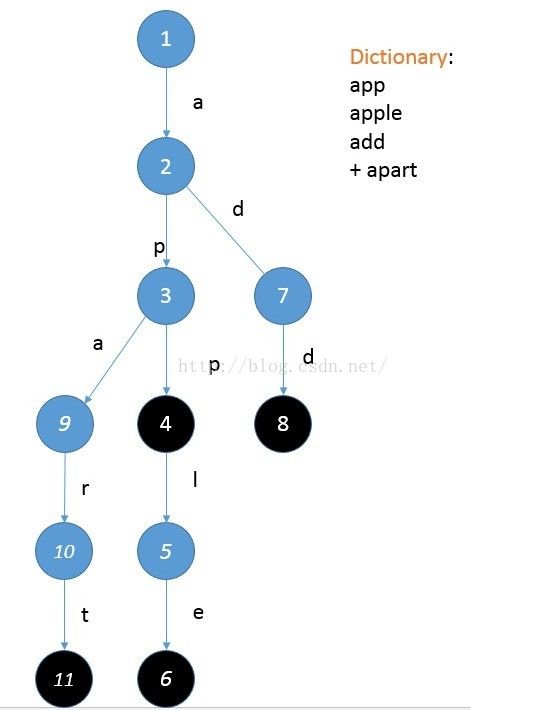
对于从树的根节点走到每一个黑色节点所经过的路径，将路径上的字母都连起来，就都对应着词典中的一个单词。

从上图可以知道，开始从1号节点走"a"这一条边就可以走到2号节点，然后从2号节点走"p"这一条边可以走到3号节点，如果没路可走就需要添加一条从3号节点出发且标记为"p"的边才可以接着往下走，然后我最后到达的这个结点标记为黑色就可以往树里添加一个新的单词了。

接下来，看看trie tree的性能，如果是一个有10W个单词的词典，每个单词的长度不超过10的话，这棵树会有多大？

假设我已经将前三个单词构成了这样一棵树，那么我要添加一个新的单词的时候，最坏情况是这个单词和之前的三个单词都没有公共前缀，那么这个新的单词的长度如果是5的话，我就至少要添加5个结点到树中才能够继续表示这个词典。而如果每次都是最坏情况的话，这棵树最多也就100W个结点。最坏情况是不可能次次都发生的！毕竟字母表也才26个字母。

接下来，看看如何运用。以3号节点为例子，我从根节点先走"a"然后走"p"到达这个结点，而且以这个结点为根的子树里所有标记结点都是以"ap"为前缀的单词，而且所有以"ap"为前缀的单词都在以这个节点为根的子树里。但是仅仅这样还是不够的，如果每次给个字符串都很短的时候，还是要扫描这棵树的很大一部分，也就是说虽然平均时间复杂度降低了，但是最坏情况时间复杂度还是很高。

优化。不妨称以T为根的子树中标记节点的个数为L[T]，既然我要统计某个L[T1]，而这个结点是不确定的，我就一次性把所有结点的L[T]求出来。我在最开始置所有L[T]=0，然后每次添加一个新的单词的时候，都将它经过的所有结点的L[T]全部+1，这样我构建完这棵Trie树的时候，我也就能够同时统计到所有L[T]了。

代码实现：

struct Node{
	int cnt;	//多少个前缀以这个节点结尾 
	int nx[26];	//下个字母
	void init()	//初始化节点
	{
		cnt = 0;
		memset(nx, -1, sizeof nx);
	}
}node[MAXN];

void insert(char *s){
	int i = 0, p = 0;//p 母节点
	while (s[i])
	{
		int x = s[i] - 'a';
		if (node[p].nx[x] == -1)
		{
			node[len].init();
			node[p].nx[x] = len++;
		}
		p = node[p].nx[x];
		++node[p].cnt;
		++i;
	}
}

void query(char *s){
	int i = 0, p = 0;
	while (s[i])
	{
		int x = s[i] - 'a';
		if (node[p].nx[x] == -1)
		{
			puts("0");
			return;
		}
		p = node[p].nx[x];
		++i;
	}
	cout << node[p].cnt << endl;
}

void hiCode(){
	int n, m;
	char s[20];
	cin >> n;
	len = 1;
	node[0].init();
	while (n--){
		cin >> s;
		insert(s);
	}
	cin >> m;
	while (m--)
	{
		cin >> s;
		query(s);
	}
}

方法二

struct Nodes{
	int n;
	Nodes*leafs[26];
	Nodes(int n_) :n(n_){ memset(leafs, 0, sizeof(leafs)); }//结构体构造函数
};
void insert(Nodes** head, const char* s, int len){
	if (len == 0){
		if (*head == NULL)
			*head = new Nodes(1);
		else
			(*head)->n++;
		return;
	}
	if (*head == NULL){
		*head = new Nodes(1);
	}
	else
		(*head)->n++;
	insert(&(*head)->leafs[*s - 'a'], s + 1, len - 1);
}
int search(Nodes *head, const char *s, int len){
	if (len == 0){
		if (head == NULL)
			return 0;
		else return head->n;
	}
	if (head == NULL)
		return 0;
	return search(head->leafs[*s - 'a'], s + 1, len - 1);
}
int main(){
	string s;
	int n;
	cin >> n;
	Nodes* head = 0;
	while (n--) {
		cin >> s;
		insert(&head, s.c_str(), s.length());
	}
	cin >> n;
	while (n--) {
		cin >> s;
		cout << search(head, s.c_str(), s.length()) << endl;
	}
	return 0;
}