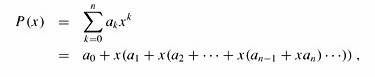字符串匹配之RK算法

Rabin-Karp字符串匹配算法,

 

实际应用中，Rabin和Karp建议的字符串匹配算法能较好地运行，还可以归纳出有关问题地其他算法，如二维模式匹配。

 

假定字符集Σ ＝{0, 1, 2, ……， 9}， 每一个字符对应一个十进制数字

（一般情况, 假定每个字符是基数为d的表示法中的一个数字， d=|Σ|。)可以用一个长度为k的十进制数字来表示由k个连续字符组成的字符串.

因此，字符串"31415" 对应于十进制数31415

已知模式P[1..m]，设p表示其相应十进制数地值，类似地， 对于给定的文本T[1..n]. 用

t_s 表示长度为m的子字符串 T[ s + 1 ‥ s + m]（ s = 0, 1, . . . , n – m），  t_s = p 当且仅当 [ s + 1 ‥ s + m] = P[1 ‥ m]; 因此s是有效位移当且仅当 t_s = p. (暂不考虑p和 t_s 可能是很大的数的情况)。

可以用霍纳规则(Horner’s rule) 在Θ(m) 的时间内计算p的值

p = P[m] + 10 (P[m - 1] + 10(P[m - 2] + · · · + 10(P[2] + 10P[1]) )).

 

Horner’s rule

类似地，可以在 Θ( m)时间内，根据T[1..m]计算出 t ₀ 的值。

如果能在总共Θ(n - m + 1) 时间内计算出所有的t_s 的值，那么通过把p值与每个t_s（有n－m＋1个）进行比较，就能够在Θ(m) + Θ(n - m + 1)= Θ(n) 时间内求出所有有效位移。（计算出1个t_s 就跟p比较，处理结果。）

为了在Θ(n - m) 时间内计算出剩余的值t₁, t₂, . . . , t_n-m 可以在常数的时间内根据t_s计算出t_s+1，先看例子，假如m = 5，t_s = 31415, 我们去掉高位数字T [s + 1] = 3，然后在加入一个低位数字T [s + 5 + 1]（假设为2)，得到：

t_s+1 = 10(31415 - 10000 • 3) + 2 = 14152.

总结出公式：      ——公式1

如果预先计算出10 ^{m -1}（通过数论中的技术可以在 O(lg m)完成, 在这里只需简单地在 O( m）时间内计算出就可以)。那么就可以在常数时间计算出 t_{s +1}

因此，可以在Θ(m)时间内计算出p和t_0。然后在Θ(n - m + 1)时间内计算出t₁, . . . , t_n-m 并完成匹配。

现在来解决唯一的问题，就是计算中p和t_s的值可能太大，超出计算机字长，不能方便地进行处理。如果p包含m个字符，那么， 关于在p上地每次算术运算需要“常数”时间这一假设就不合理了，幸运的是，对这一问题存在一个简单的补救方法，对一个合适的模q来计算p和t_s的模，每个字符是一个十进制数，因为p和t₀ 以及公式1计算过程都可以对模q进行，所以可以在Θ(m)时间内计算出模q的p值，在Θ(n - m + 1)时间内计算出模q的所有t_s值，通常选模q为一个素数，使得10q正好为一个计算机字长，单精度算术运算就可以执行所有必要的运算过程。 一般情况下，采用d进制的字母表{0, 1, . . . , d - 1}, 所选的q要满足d*q < 字长，调整公式1， 使其为：

其中的 h = d ^{m -1} (mod q)

但是加入模q后，由t_s ≡ p (mod q)不能说明 t_s = p. 但t_s !=p (mod q), 可以说明 t_s ≠ p,

因此当 t_s ≡ p (mod q)时， 再用朴素的字符串匹配算法验证 t_s = p。. 如果q足够大，可以期望伪命中很少出现。

 

 

算法

RABIN-KARP-MATCHER(T, P, d, q)

 1 n ← length[T]

 2 m ← length[P]

 3 h ← dm-1 mod q

 4 p ← 0

 5 t0 ← 0

 6 for i ← 1 to m           

 7     do p ← (dp + P[i]) mod q

 8        t0 ← (dt0 + T[i]) mod q

 9 for s ← 0 to n - m       

10     do if p = ts

11           then if P[1 ‥ m] = T [s + 1 ‥ s + m]

12                   then print "Pattern occurs with shift" s

13        if s < n - m

14           then ts+1 ← (d(ts - T[s + 1]h) + T[s + m + 1]) mod q

 

#include<iostream>
#include<vector>
#include<string>

#define q 144451
#define d 26

using namespace std;

int RK(const string &T,const string &P){
    int m=T.length(),n=P.length();
    unsigned int h=1, t=0, p=0;

    for(int i=0;i<n-1;++i)
        h=(h*d)%q;

    for(int i=0;i<n;++i){
	t=(d*t+T[i])%q;
	p=(d*p+P[i])%q;
    }
	
    for(int i=0;i<m-n;++i){
        if(t==p&&T.substr(i,n)==P)
            return i;
	t=(d*(t-h*T[i]%q+q)+T[i+n])%q;
    }
    return -1;
}