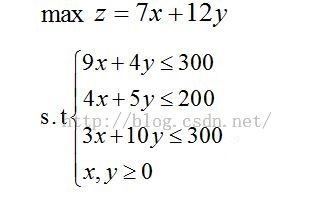MATLAB求解线性规划(含整数规划和0-1规划)问题
线性规划是数学规划中的一类最简单规划问题,常见的线性规划是一个有约束的,变量范围为有理数的线性规划。如:
对于这类线性规划问题,数学理论已经较为完善,可以有多种方法求解此类问题。但写这篇文章的目的并不是为了介绍数学理论,我们这里主要讲解如果利用工具求解这一类线性规划问题。
最著名,同时也是最强大的数学最优化软件是LINGO/LINDO软件包,它能够求解多种的数学规划问题,同时还提供了多种的分析能力。但LINGO软件并不容易上手,同时,应用LINGO的场合一般是大规模的线性规划问题,小小的线性规划完全可以不使用它。一个更受科研人员欢迎的数学软件是MATLAB,它以功能强大而称著,并有数学软件中的“航空母舰”之称。我们这里就是要学习使用MATLAB软件求解线性规划(含整数规划和0-1规划)问题。
为了使得不熟悉MATLAB的人员也能够使用MATLAB进行线性规划问题求解,本文将对MATALB中使用到的函数和过程以及结果进行详细的分析,最后会对每一个问题都给出一个可以完全“套用”的MATLAB程序。
我们首先从上面的线性规划问题开始,为了便于表达,将上面的式子写成矩阵形式:
于是约束就表达为了一个不等式。
求解MATLAB线性规划时,最常用的函数是linprog函数,下面来介绍一下这个函数的使用。
打开MATLAB帮助文档(PS:帮助文档的内容是最全的,只要你的英文过了专业8级),可以看到linprog函数求解的是具有如下标准形式的线性规划:
公式中各符号的意义是自明的,在这里简单介绍下,首先MATLAB中求解的是目标函数是最小值的问题,但如果我们的目标函数是求最大值,可以通过对目标函数中每一项中乘以-1,将求最大值问题转化为求最小值问题;A,b分别为不等式约束中的系数矩阵。Aeq和beq分别为等式约束中的系数矩阵,lb,和ub分别为每个变量的上下区间;最后f为目标函数中各变量的系数矩阵。
现在,是时候动动手,使用MATLAB编写代码求解这个线性规划了。MATLAB代码如下所示:
f=[-7,-12]; A=[9 4;4 5;3 10]; b=[300;200;300]; lb=zeros(2,1);% 生成一个2行1列的全1矩阵 [x,fval]=linprog(f,A,b,[],[],lb,[])
我们来解释下linprog函数中每参数的意义,linprog中的一个原型如下:
[x,fval,exitflag] = linprog(f,A,b,Aeq,beq,lb,ub)
这7个参数的意义和上面f、A、b的意义是一样的。f为目标函数的系数矩阵,A为线性规划不等式约束的变量系数矩阵,b为不等式约束的资源数(如上面的[300;200;300]),这是一个N行1列的矩阵,N为变量的个数。Aeq和beq是相应等式约束的变量系数矩阵和资源数(很明显,上面的例子中并没有等式约束)。lb和ub分别为保变量的上下区间。在上面的例子中,x和y和最小值都为0但都无最大值约束。而linprog的返回值x为求得的各变量的值,这是一个向量,fval为最优化的值,一般是一个标量,exitflag意为函数的退出标志。
上面所示的代码[x,fval]=linprog(f,A,b,[],[],lb,[])中,[]代表不存在或空,因为在上面的例子中不存在等式约束,所以Aeq和beq的位置为[]。而ub也为空,是因为变量没有最大值约束。
运行上面的程序,行到结果为:
x =
20.0000
24.0000
fval =
-428.0000
解释为:
当x=20,y=24时,可以求得最优化的值,最大值为428(因为这里的求目标最大值,但MATLAB只能求目标函数最小值,所以对目标函数进行了乘-1处理,所以也要对最后的结果乘以-1才是目标函数所求).
上面解决了简单的线性规划问题的求解,线性规范有两种比较特殊的情况,即整数规划和0-1整数规划。在之前(不知MATLAB几之前……),MATLAB是不能直接求解这两种规划的,bintprog函数可以用来求0-1整数规划,但求解过程比较麻烦,而且最新版的MATLAB已经遗弃了这个函数,同时提供了一个比较新的、专用于求解整数规划和0-1整数规划的函数——intlinprog。intlinprog的一个原型为:
[x,fval,exitflag]= intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
该函数的使用和linprog函数的使用十分相似,其仅仅在linprog函数的基础上多了一个参数——intcon。我们来通过下面的例子来学习该参数的意义。
在这里例子中,变量的取值范围不再是有理数集,而是整数集。求解此规划问题的MATLAB程序如下:
f_13=[-1,-1]; ic_13=[1,2]; A_13=[-4,2;4,2;0,-2]; b_13=[-1;11;-1]; lb_13=zeros(2,1); [x_13,fval_13,flag_13]=intlinprog(f_13,ic_13,A_13,b_13,[],[],lb_13,[])
在函数intlinprog中,intcon的意义为整数约束变量的位置。如上例中,因为x1和x2都要是整数,intcon参数位置ic_13的值为[1,2]。这个位置是按照目标函数和约束条件中变量位置来排列的。如果上式中仅有x2为整数约束,那么ic_13的值应该为2。
需要说明的是,intlinprog函数在比较旧版本是不支持的(笔者使用的是MATLAB2014B),如果你发现你现在的MATLAB没有intlinprog函数,请不要吃惊,因为一直以来,MATLAB都是无法直接求解整数规划的,但今时已经不同往日了。
现在又有了一个新问题,我们解决了在MATLAB上求解一般的整数规划问题,但要是遇到0-1整数规划问题呢?到这里,我们只要转换一下思维,就可以利用MATLAB求解0-1整数规划了,这里先卖个关子,请大家看下面的例子是怎么用MATLAB求解0-1整数规划的。
MATLAB程序如下:
f_12=[7 5 9 6 3]; ic_12=[1,2,3,4,5]; A_12=[56,20,54,42,15;1,4,1,0,0;-1,-2,0,-1,-2]; b_12=[100;4;-2]; lb_12=zeros(5,1); ub_12=ones(5,1); [x_12,fval_12,flag_12]=intlinprog(f_12,ic_12,A_12,b_12,[],[],lb_12,ub_12)
有木有发现在,与上面整数规划不同的地方只有一个,就是多了ub_12=ones(5,1),也就是说求解0-1整数规划只要在求解整数规划的基础上加上一个对变量最大值约束为1就行了,有木有恍然大悟的感觉???
后面两个程序并没有给出程序运行的结果,因为笔者坚信学习最好的方式就是“动手”。^_^