USACO算法系列十四——fence
题目:http://www.nocow.cn/index.php/Translate:USACO/fence
看完这道题目的第一想法就是,遍历所有的边,而且每一条边的经过次数只能一次。是离散数学里面的图论的欧拉通路问题,在这里充分体现了数学的重要性。
定理:无向图G有欧拉通路的充分必要条件是G为连通图,并且G仅有两个奇度结点或者无奇度结点。
(1)当G是仅有两个奇度结点的连通图时,G的欧拉通路必以此两个结点为端点。
(2)当G是无奇度结点的连通图时,G必有欧拉回路。
因此第一个点,要么是最小的度数为奇数的点(如果存在),否则为是下标最小的点。
我的想法是采用深度遍历的回溯方法,如果不能一次遍历完所有的边,则回退到上一个节点,直到搜索到结果为止,代码如下:
#include <iostream> #include <fstream> #define SIZE 501 using namespace std; int map[SIZE][SIZE] = {0}; int vertex[SIZE] = {0}; int path[1025] = {0}; int length = 0; int main() { ifstream fin("fence.in"); ofstream fout("fence.out"); //读入数据 int n; fin >> n; for (int i=0; i < n; i ++) { int s=0; int e=0; fin >> s >> e; vertex[s] ++; vertex[e] ++; map[s][e] ++; map[e][s] ++; } int index = 1; //找出第一个点的度为奇数的点 for (int i=1; i < SIZE; i ++) { if ((vertex[i]&1) == 1) { index = i; break; } } //记录路径 path[length] = index; length ++; bool flag = false; //计算路径 while (length <= n) { int start = 0; if (flag) { //回退 if (length > 1) { start = path[length-1]; index = path[length-2]; map[index][start] ++; map[start][index] ++; length --; } } flag = true; //深度遍历 for (int i=start+1; i < SIZE; i ++) { if (map[index][i] > 0) { map[index][i] --; map[i][index] --; index = i; path[length] = index; length ++; flag = false; break; }//end if }//end for }//end while for (int i=0; i < length; i ++) { fout << path[i] << endl; } return 0; }
可惜的是,时间一直都是超时的,通不过去。
看了USACO的提示,他也是采用深度遍历的方法,然后将结果逆序保存打印。但是这个深度遍历跟我的那个方法有着本质的区别,他的深度遍历是遍历边,而我的深度遍历是深度搜索,时间复杂度不在一个数量级上。很让我奇怪的是,为什么简简单单的一次深度遍历边,然后逆序保存节点就可以找出欧拉通路呢?
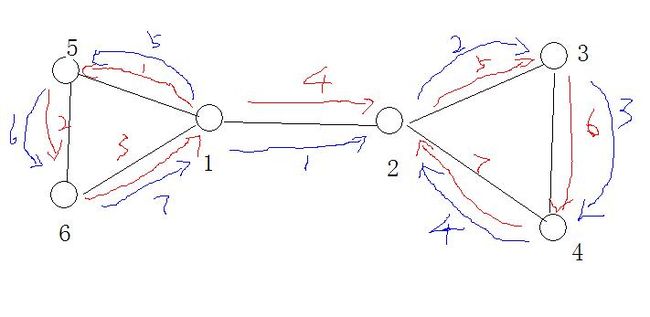
举个例子:
正确的欧拉通路顺序是红色的,但是按节点下标的深度遍历的顺序是蓝色方式。很显然如果从方向来看的话,二者的结果肯定是不同的。
我们先看一下代码入下:
#include <iostream> #include <fstream> #define SIZE 501 using namespace std; int map[SIZE][SIZE] = {0}; int vertex[SIZE] = {0}; int path[1025] = {0}; int length = 0; void find(int index) { for(int i=0; i < SIZE; i ++ ) { if (map[index][i] > 0) { map[index][i] --; map[i][index] --; find(i); } }//end for path[length] = index; length ++; }//end find int main() { ifstream fin("fence.in"); ofstream fout("fence.out"); //读入数据 int n; fin >> n; for (int i=0; i < n; i ++) { int s=0; int e=0; fin >> s >> e; vertex[s] ++; vertex[e] ++; map[s][e] ++; map[e][s] ++; } int index = 0; //找出第一个点的度为奇数的点 for (int i=1; i < SIZE; i ++) { if ((vertex[i]&1) == 1) { index = i; break; } } if (index ==0) { for (int i=1; i <SIZE; i ++) { if (vertex[i] > 0) { index = i; break; } } } find(index); for (int i=length-1; i >=0; i --) { fout << path[i] << endl; } return 0; }
按照程序的执行思路跑一遍,可以得到如下步骤:
find(1):
map[1][2] = 1;
find(2)
map[2][3] = 1;
find(3)
map[3][4]=1;
find(4)
map[4][2]=1;
find(2) //此时所有的map[2][i] = 0
记录2
return;
所有map[4][i]=0
记录4
return
map[3][i] =0
记录3
return;
所有map[2][i]=0
记录2
return
map[1][5] = 1;
find(5)
map[5][6] = 1
find(6)
map[6][1] = 1;
find(1);
ALL map[1][i]=0;
记录1
return
记录6
return
记录5
return
记录1
return;
逆序打印结果是1 5 6 1 2 3 4 2,就是正确答案。
本来我也想不明白其中的缘由,但是如果把问题理解为实际上我们就是寻找一个点序列,使得按照这个点序列遍历边,能经过每一条边,并且只有一次。根据欧拉通路的从要条件,我们可以很明确的得到第一个点(起点)S。那么我们要确定的是下一个欧拉通路的点P,是与起点连接的点中的哪一个?那我们可以想一下,哪一个点是下一个欧拉点P呢?就是沿着S P然后经过深度遍历,能够将所有的边都遍历到的点就是欧拉点,就是经过SP往下深度遍历以后,所有MAP【i】【j】=0。
运行结果如下:
Executing... Test 1: TEST OK [0.000 secs, 3996 KB] Test 2: TEST OK [0.000 secs, 3996 KB] Test 3: TEST OK [0.011 secs, 3996 KB] Test 4: TEST OK [0.011 secs, 3996 KB] Test 5: TEST OK [0.011 secs, 3996 KB] Test 6: TEST OK [0.000 secs, 3996 KB] Test 7: TEST OK [0.011 secs, 3996 KB] Test 8: TEST OK [0.032 secs, 3996 KB] All tests OK.