计算几何基础
nyoj67求三角形面积
向量乘积(叉积)的一半 = 三角形面积 ab *ac/2
nyoj68三点顺序,叉积判断向量相对位置。
ab x ac > 0 即 x1 * y2 >x2 * y1
即 x1/y1 > x2 / y2; 也就是斜率的比较,也可以这么理解吧。
nyoj1016 叉积判断直线相交。
参考文章http://www.cnblogs.com/jbelial/archive/2011/08/04/2127487.html
德莱联盟
时间限制:
1000 ms | 内存限制:
65535 KB
难度:
1
- 描述
-
欢迎来到德莱联盟。。。。
德莱文。。。
德莱文在逃跑,卡兹克在追。。。。
我们知道德莱文的起点和终点坐标,我们也知道卡兹克的起点和中点坐标,问:卡兹克有可能和德莱文相遇吗?,并且保证他们走的都是直线。
- 输入
-
几组数据,一个整数T表示T组数据
每组数据 8个实数,分别表示德莱文的起点和终点坐标,以及卡兹克的起点和终点坐标 - 输出
- 如果可能 输出 Interseetion,否则输出 Not Interseetion
- 样例输入
-
2 -19.74 7.14 22.23 -27.45 -38.79 -5.08 47.51 34.01 -8.61 9.91 -32.47 6.47 -3.81 -16.1 7.82 -6.37
- 样例输出
-
Interseetion Not Interseetion
首先利用向量构造出的”矩阵“快速排除不可能相交的情况,然后利用向量叉积判断直线相对位置的方法,判断是否相交
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<vector>
#include<cmath>
using namespace std;
typedef long long ll;
struct Point{
double x,y;
};
double mult(Point a, Point b, Point c)
{
return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}
//aa, bb为一条线段两端点 cc, dd为另一条线段的两端点 相交返回true, 不相交返回false
bool intersect(Point aa, Point bb, Point cc, Point dd)
{
if ( max(aa.x, bb.x)<min(cc.x, dd.x) )
return false;
if ( max(cc.x, dd.x)<min(aa.x, bb.x) )
return false;
if ( max(aa.y, bb.y)<min(cc.y, dd.y) )
return false;
if ( max(cc.y, dd.y)<min(aa.y, bb.y) )
return false;
//如果 向量 ac ab 和 ad ab反向 或者共线,
//并且 向量 ca cd 和 cb cd 反向 则判断相交(跨立)
if(mult(cc,bb,aa) * mult(dd,bb,aa) <= 0
&& mult(aa,dd,cc) * mult(bb,dd,cc) <= 0)
return true;
return false;
//第二种方法 如果本该同向的向量反向了 直接return false;
/*if ( mult(cc, bb, aa)*mult(bb, dd, aa)<0 )
return false;
if ( mult(aa, dd, cc)*mult(dd, bb, cc)<0 )
return false;
return true;*/
}
double dis(Point& a,Point& b){
return sqrt((a.x - b.x)*(a.x - b.x) +(a.y - b.y)*(a.y - b.y) );
}
int main(){
int T; scanf("%d",&T);
while(T--){
Point a,b,c,d;
cin>>a.x>>a.y>>b.x>>b.y>>c.x>>c.y>>d.x>>d.y;
if(intersect(a,b,c,d))
printf("Interseetion\n");
else
printf("Not Interseetion\n");
}
}
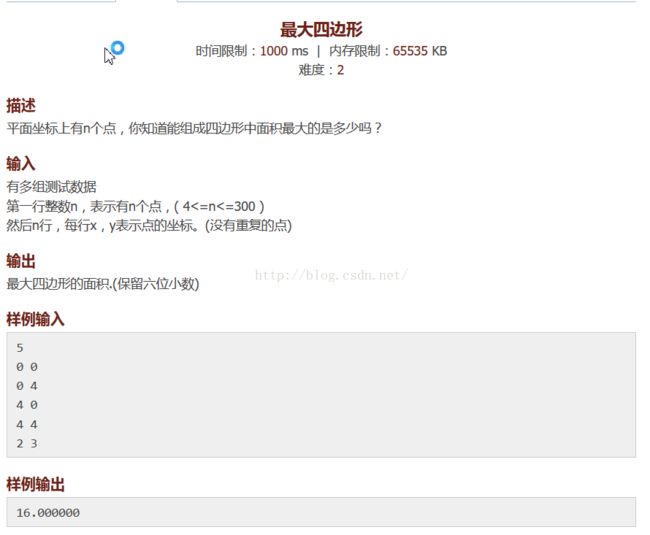
nyoj952 叉积求面积
可以通过向量的叉积运算求出两个三角形的面积相加得到四边形的面积。
如何确定可以组合的两个三角形呢? 找到他们的公共边,然后通过叉积判断剩下的两个点是否在边的两侧即可。
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
struct point{
double x,y;
}po[333];
double mul(point a,point b,point c){
return (a.x - c.x)*(b.y - c.y) - (b.x - c.x)*(a.y-c.y);
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
for(int i=0;i<n;i++)
scanf("%lf%lf",&po[i].x,&po[i].y);
double ans = 0;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
double m1 = 0,m2 = 0;
for(int k=0;k<n;k++){
if(k == i || k == j) continue;
double l = mul(po[k],po[i],po[j]);
if(l < 0){
//cout<<"sd"<<endl;
m1 = max(m1,abs(mul(po[i],po[j],po[k]))/2);
}
else if( l > 0){
//cout<<"rr"<<endl;
m2 = max(m2,abs(mul(po[i],po[j],po[k]))/2);
}
}
if(m1!=0 && m2 != 0){
ans = max(ans,m1+m2);
}
}
}
printf("%.6f\n",ans);
}
return 0;
}
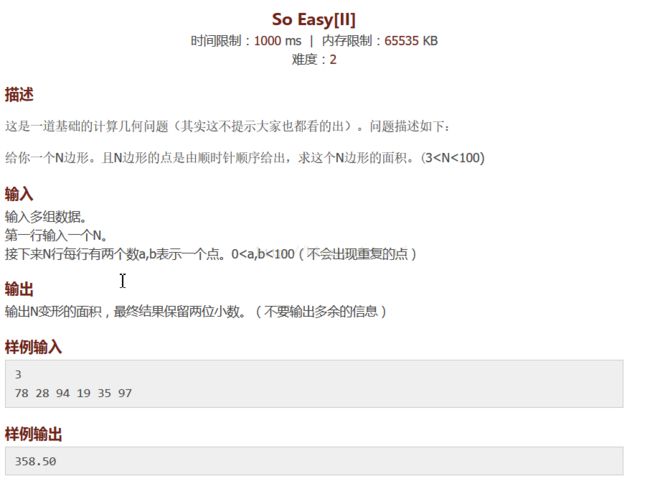
nyoj1011 ,简单求面积
//顺时针给出的点,直接以第一个点为构成多边形的所有三角形的顶点,求面积和即可
double ans = 0;
for(int i=2;i<n;i++){
ans += (mul( po[i-1], po[i],po[0]))/2; //矢量三角形面积
}
printf("%.2f\n",abs(ans)); //求绝对值
nyoj1132 判断线段相交,求交点。
开始直接裸奔,幻想着随便一写就1A了,然后wa了4次。。
利用叉积判断是否相交是没有问题的,求焦点的时候要把问题考虑全面。在我的代码中,我将两条直线转换成y = kx + b我熟悉的点斜式。
然后做差求交点。 wa了几次发现代码中的小问题。
1. 斜率不存在时 出现除零错误。
2. 题目要求说两个线段不会重合,但是是可以平行的,当平行的时候可能出现“首尾相连”;
<pre name="code" class="cpp">#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
struct point{
double x,y;
}po[120];
double mul(point a,point b,point c){
return (a.x - c.x)*(b.y - c.y) - (b.x - c.x)*(a.y-c.y);
}
bool judge(point a,point b,point c,point d){
if(max(a.x,b.x) < min(c.x,d.x))
return false;
if(max(c.x,d.x) < min(a.x,b.x))
return false;
if(max(a.y,b.y) < min(c.y,d.y))
return false;
if(max(c.y,d.y) < min(a.y,b.y))
return false;
if(mul(a,c,b) * mul(a,d,b) <=0 &&
mul(a,d,c) * mul(b,d,c) <=0)
return true;
return false;
}
int main(){
int n;
scanf("%d",&n);
for(int i=0;i<n;i++){
point a,b,c,d;
scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y
,&b.x,&b.y,&c.x,&c.y,&d.x,&d.y);
if(judge(a,b,c,d)){
double x1,y1;
if(b.x == a.x){ // 第一条线段没有斜率
double k2 = (d.y - c.y)/(d.x - c.x);
double b2 = d.y - d.x * k2;
x1 = b.x;
y1 = k2 * x1 + b2;
printf("yes %.1f %.1f\n",x1,y1); continue;
}
else if(c.x == d.x){ //第二条无斜率
double k1 = (b.y - a.y)/(b.x - a.x); //除 0
double b1 = b.y - b.x * k1;
x1 = c.x;
y1 = k1 * x1 + b1;
printf("yes %.1f %.1f\n",x1,y1); continue;
}
double k1 = (b.y - a.y)/(b.x - a.x);
double b1 = b.y - b.x * k1;
double k2 = (d.y - c.y)/(d.x - c.x);
double b2 = d.y - d.x * k2;
if(k1 == k2){ //找重合的点。
if(a.x == c.x && a.y == c.y)
x1 = a.x,y1 = a.y;
else if(a.x == d.x && a.y == b.y)
x1 = a.x,y1 = a.y;
else if(b.x == c.x && b.y == c.y)
x1 = b.x,y1 = b.y;
else if(b.x == d.x && b.y == d.y)
x1 = b.x,y1 = b.y;
else{
printf("no\n"); continue;
}
printf("yes %.1f %.1f\n",x1,y1);continue;
}
x1 = (b1 - b2)/(k2-k1); //除 0
y1 = x1 * k1 + b1;
printf("yes %.1f %.1f\n",x1,y1);
}
else
puts("no");
}
return 0;
}