算法学习之“Omega“、“Theta”和“Little Oh”
一、An asymptotical lower bound - Omega
The big oh notation introduced in the preceding section is an asymptotic upper bound. In this section, we introduce a similar notation for characterizing the asymptotic behavior of a function, but in this case it is a lower bound.
Definition (Omega) Consider a function f( n) which is non-negative for all integers. We say that `` f( n) is omega g( n),'' which we write
, if there exists an integer
and a constant c>0 such that for all integers
,
.
The definition of omega is almost identical to that of big oh. The only difference is in the comparison--for big oh it is 
; for omega, it is . All of the same conventions and caveats apply to omega as they do to big oh.
二、“Theta” 和 “Little Oh”
This section presents two less commonly used forms of asymptotic notation. They are:
- A notation,
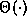, to describe a function which is both O(g(n)) and 
, for the same g(n). (Definition 
). - A notation,
, to describe a function which is O(g(n)) but not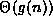 
, for the same g(n). (Definition ).
Definition (Theta) Consider a function f( n) which is non-negative for all integers, if and only if f( n) is O( g( n)) and f( n) is
Recall that we showed in Section that a polynomial in n, say 
, is 
. We also showed in Section that a such a polynomial is 
. Therefore, according to Definition , we will write 
.
Definition (Little Oh) Consider a function f( n) which is non-negative for all integers
Little oh notation represents a kind of loose asymptotic bound in the sense that if we are given that f(n)=o(g(n)), then we know that g(n) is an asymptotic upper bound since f(n)=O(g(n)), but g(n) is not an asymptotic lower bound since f(n)=O(g(n)) and 
implies that 
.
For example, consider the function f(n)=n+1. Clearly, 
. Clearly too, 
, since not matter what c we choose, for large enough n, 
. Thus, we may write 
.