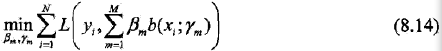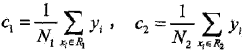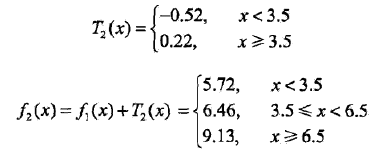提升方法 - 2 - 前向分布算法和提升树
声明:
1,本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结,不得用作商用,欢迎转载,但请注明出处(即:本帖地址)。
2,由于本人在学习初始时有很多数学知识都已忘记,所以为了弄懂其中的内容查阅了很多资料,所以里面应该会有引用其他帖子的小部分内容,如果原作者看到可以私信我,我会将您的帖子的地址付到下面。
3,如果有内容错误或不准确欢迎大家指正。
4,如果能帮到你,那真是太好了。
上一节讲解了Adaboost算法,下面我们要通过Adaboost的另一种解释引申到前向分布算法,进而通过上面这些引出提升树,最后学习梯度提升。
Adaboost算法的另一种解释
Adaboost算法还有另一种解释,即:可以认为Adaboost算法是“模型为加法模型、损失函数为指数函数、学习算法为前向分布算法”时的二类分类学习方法。
前向分布算法
在Adaboost算法中,我们的最终目的是通过构建弱分类器的线性组合:
来得到最终分类器。
而我们在看看加法模型:
其中,b(x; rm)为基函数,rm是基函数的参数,βm为基函数的系数。
显然式8.6是一个加法模型。
对于加法模型,在给定训练数据及损失函数L(y, f(x))的条件下,学习加法模型f(x)就成为经验风险极小化损失函数极小化问题:
但这是一个复杂的优化问题。
前向分布算法(forward stagewise algorithm)求解这一优化问题的想法是:
因为学习的是加法模型,那如果能够从前向后,每一步只学习一个基函数及其系数,然后逐步逼近优化目标式8.14,那么就可以简化优化的复杂度。
具体的,每步只需优化如下损失函数:
于是,前向分布算法总结如下:
输入:
训练数据集T ={(x1,y1), (x2, y2), ..., (xN, yN)};损失函数L(y, f(x));基函数集{b(x; r)};
输出:
加法模型f(x)
解:
1,初始化f0(x)= 0
2,对m = 1, 2,.., M
a,极小化损失函数
得到参数βm, rm
b,更新
![]()
3,得到加法模型
这样,前向分布算法将同时求解从m=1到M的所有参数βm, rm的优化问题简化为逐次求解各个βm, rm的优化问题。
提升树
提升树是以决策树为弱分类器的提升方法,通常使用CART树。
提升树被认为是统计学习中性能最好的方法之一。
提升树模型
提升树方法实际采用:加法模型 + 前向分布算法 + CART树(基函数)。
在Adaboost的例子中看到的弱分类器x<v或x>v,可以看做是由一个根结点直接连接两个叶结点的简单决策树,即所谓的决策树桩。提升树模型可以表示为决策树的加法模型:
其中,T(x,θm)表示决策树;θm为决策树的参数;M为树的个数。
提升树算法
既然提升树采用前向分布算法,那就将前向分布算法的步骤的思想套用到这里吧。
首先,确定初始提升树f0(x)= 0,于是第m步的模型就是:
![]()
其中fm-1(x)是当前模型,通过经验风险极小化确定下一棵决策树的参数θm,
由于树的线性组合可以很好的拟合训练数据,即使数据中的输入与输出之间的关系很复杂也可以很好的拟合。所以提升树是一个高功能的学习算法。
下面讨论针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。包括用平方误差损失函数的回归问题,用指数损失函数的分类问题,以及用一般损失函数的一般决策问题。
对于二类分类问题,提升树算法只需将Adaboost中的弱分类器限制为二类分类树即可,这里不再细数。下面叙述回归问题的提升树:
已知一个训练数据集T={(x1,y1), (x2, y2), ..., (xN, yN)},x∈X⊆ Rn,X为输入空间,yi∈Y⊆ R,Y为输出空间。如果将输入空间X划分为J个互不相交的区域R1, R2, ..., RJ,并且在每个区域上确定输出的常亮cj,那么树可以表示为:
其中,参数θ={(R1,c1), (R2, c2), ..., (RJ, cJ)}表示树的区域划分和各区域上的常数,J是回归树的复杂度即叶子节点的个数。
对8.26式举个例子的话就像下面这样:
回归问题提升树使用以下前向分布算法:
在前向分布算法的第m步,给定当前模型fm-1(x),需求解
即得到第m棵树的参数。
当采用平方误差损失函数时,
L(y,f(x)) = (y - f(x))2
其损失变为:
L(y,fm-1(x) + T(x;θm))
=[y - fm-1(x) - T(x;θm)]2
=[r - T(x;θm)]2
这里
r= y - fm-1(x) (8.27)
是当前模型拟合数据的残差。所以对回归问题的提升树算法来说,只需简单的拟合当前模型的残差。这样,算法是相当简单的。
现将回归问题的提升树算法叙述如下
输入:
训练数据T={(x1,y1), (x2, y2), ..., (xN, yN)},xi∈X⊆ Rn,yi∈Y⊆ R
输出:
提升树fM(x)
解:
1,初始化f0(x)= 0
2,对m = 1, 2,..., M
a,按式8.27计算残差:rmi= yi - fm-1(xi), i = 1, 2, ..., N
b,拟合残差rmi学习一个回归树,得到T(x;θm)
c,更新fm(x)= fm-1(x) + T(x;θm)
3,得到回归问题提升树
例子
已知训练数据如上表所示,x的取值范围为区间[0.5,10.5],y的取值范围为区间[5.0, 10.0],学习这个回归问题的的提升树模型,考虑只用树桩作为基函数。
解:
既然是学习出一个提升树:
那么第一步我们就要求f1(x),即回归树T1(x)。
首先,通过以下优化问题
求解训练数据的切分点s:
R1= {x | x <= s},R2 = {x | x > s}
容易求得在R1,R2内部使平方损失误差达到最小值的c1, c2为
这里N1,N2是R1,R2的样本个数。
将上面的想法应用到数据上就是:
根据所给数据,考虑如下切分点:1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5
对各切分点,不难求出相应的R1,R2, c1, c2及
如:当s=1.5时,R1={1},R2={2, 3, 4,5, 6, 7, 8, 9, 10},c1 = 5.56,c2=7.50,
m(s)= 0 + 15.72 = 15.72
现将s及m(s)的计算结果列表如下
由上表可知,当s=6.5时m(s)达到最小值,此时R1={1,2, ..., 6},R2={7, 8, 9, 10},c1=6.24,c2=8.91,所以回归树T1(x)为
用f1(x)拟合训练数据的残差见下表,表中r2i = yi - f1(xi),i=1, 2, ...,10.
用f1(x)拟合训练数据的平方损失误差:
第二步求T2(x)。方法与求T1(x)一样,只是拟合的数据是表8.4的残差。可以得到:
用f2(x)拟合训练数据的平方损失误差是
就这样继续求得
用f6(x)拟合训练数据的平方损失误差是:
假设此时已满足误差要求,那么f(x) = f6(x)即为所求提升树。
梯度提升
上面的提升树算法利用加法模型与前向分步算法实现学习的优化过程。虽然当损失函数时平方损失和指数损失函数时,每一步的优化很简单,但对于一般损失函数而言,往往每一步的优化并不那么容易。而梯度提升(gradient boosting)算法就是解决这个问题的。
梯度提升算法利用最速下降法的近似方法,其关键是利用损失函数的负梯度在当前模型的值
作为回归问题提升树算法中残差的近似值,拟合一个回归树。
梯度提升算法描述
输入:
训练数据T={(x1,y1), (x2, y2), ..., (xN, yN)},xi∈X⊆ Rn,yi∈Y⊆ R;损失函数L(y, f(x))
输出:
回归树。
解:
解释:
第1步:估计使损失函数极小化的常数值,它是只有一个根结点的树。
第2(a)步:计算损失函数的负梯度在当前模型的值,将它作为残差的估计。对于平方损失函数,它就是通常所说的残差;对于一般损失函数,它就是残差的近似值。
第2(b)步:估计回归树的叶结点区域,以拟合残差的近似值。
第2(c)步:利用线性搜索估计叶结点区域的值,使损失函数极小化。
第2(d)步:更新回归树。
第3步:得到最终的输出模型。