BZOJ 4012 HNOI 2015 开店(shop) 一道简单的点剖题

题目大意

给你一棵结点编号为 1 ~ N 的树。
每个节点有一个权值 Xi ,且每个节点的度数小于等于 3 。
每条边都有一个距离 Vi 。
现在有Q个询问，每次询问给你三个数 u , L , R , 要求输出所有权值为 L ~ R 的节点到节点 u 的距离和。
强制在线， 时间限制为 7s 。
N<=150000 Q<=200000
对于所有点的权值 Xi<=1000000000 对于每条边的距离 Vi<=1000

解题思路

看到这种树上求距离的题，就会很自然地想到点剖。然而听说这题有很多种解法，什么线段树维护虚数，分块之类的，在这里就主要介绍一下点剖的做法。

我们可以先对这一棵树先进行点剖，看一下我们需要的值应该怎样得来。
假设点 u 分别被 a1,a2,a3,......ak覆盖到 (显然 k≤logN )。然后我们分别对 ai 进行询问，对于每个重心 ai 我们只统计除了包含 u 的子树外别的子树经过 ai 到 u 的距离。什么意思呢，我们看看下面的这幅图：

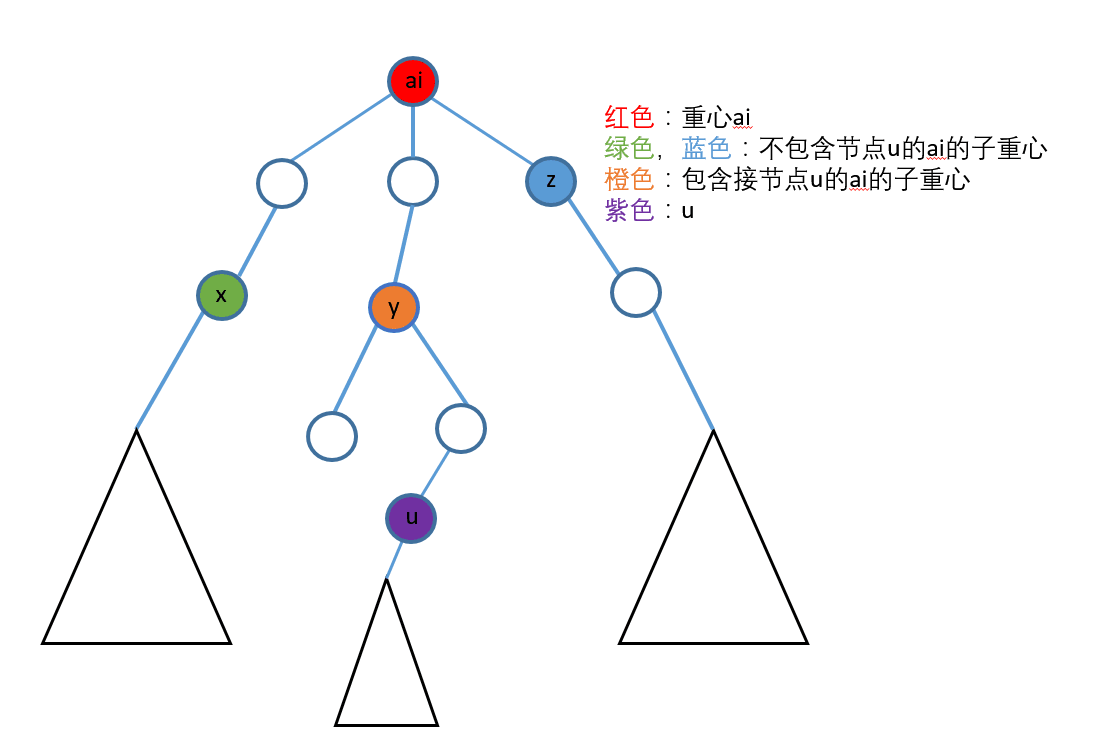
在我的定义下，子重心就是一个重心直接包含的另一些重心。

那我们应该如何计算呢？
我们设 disi 表示 i 到当前重心 ai 的距离， Counti 表示i的子树中年龄在 [L,R] 之间的点的数量， Sumi 表示i的字数中年龄在 [L,R] 之间的点的 dis 之和。

那么如上图，假设 ai 有子重心 x,y,z ,那么对于重心 ai 的答案显然等于除了包含 u (即 y )以外的子重心(即 x 和 y )到结点 u 的和。就有公式：
Ansai=Countx∗disu+Sumx+Countz∗disu+Sumz

最后在把 Ansi 累计起来就是答案。

一些小技巧

现在还有一个问题就是如何提取出 [L,R] 之间的值。很自然的就可以想到用线段树来维护。另外有一个简单的做法就是用c++自带的 vector 来维护，我们只需把每个点的年龄信息以及 dis 的前缀和记录下来。然后用下面两个c++自带的函数来减少代码量：
设p是 vector 类型
lower_bound( p.begin(),p.end(),L )意思是返回第一个大于等于 L 的位置的迭代器。
upper_bound( p.begin(),p.end(),R )意思是返回第一个大于 R 的位置的迭代器。

我们再分别把他们减去 p.begin() 就可以返回一个 int 类型的准确位置，分别设为 l,r ，那么 Count 就是 r−l+1 ， Sum 就是 r 下标的前缀和减去 l−1 下标的前缀和。具体操作可见于代码。
(如果对迭代器不了解可以上网查资料，网上有很详细的解释)

程序

//HNOI 2015 开店(shop) YxuanwKeith
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;

typedef long long LL;
const int MAXN = 2e5, MAXS = 4, MAXL = 19;

int N, Q, A, u, top, Num, L, R, D[MAXN * 2], Deep[MAXN], Age[MAXN], Son[MAXN][MAXS];
int tot, Last[MAXN], Next[MAXN * 2], Go[MAXN * 2], Val[MAXN * 2], Pre[MAXN];
int Min, Root, All, Flag[MAXN], Size[MAXN], Max[MAXN], Dis[MAXN], Fa[MAXN][MAXL + 1];
LL Ans;

vector<int> VAge[MAXN][MAXS], VSon[MAXN][MAXS];
vector<LL> VSum[MAXN][MAXS];

void Link(int u, int v, int val) {
    Next[++ tot] = Last[u], Last[u] = tot, Go[tot] = v, Val[tot] = val;
}

bool cmp(int u, int v) { return Age[u] < Age[v];}

void GetDeep(int Now, int fa, int val) {
    Deep[Now] = Deep[fa] + 1, Fa[Now][0] = fa, Dis[Now] = val;
    for (int p = Last[Now]; p; p = Next[p]) 
        if (Go[p] != fa) GetDeep(Go[p], Now, val + Val[p]);
}

void GetFa() {
    for (int i = 1; i <= MAXL; i ++)
        for (int j = 1; j <= N; j ++)
            Fa[j][i] = Fa[Fa[j][i - 1]][i - 1];
}

int Lca(int u, int v) {
    if (Deep[u] < Deep[v]) swap(u, v);
    for (int i = MAXL; i + 1; i --) 
        if (Deep[Fa[u][i]] >= Deep[v]) u = Fa[u][i];
    if (u == v) return u;
    for (int i = MAXL; i + 1; i --)
        if (Fa[u][i] != Fa[v][i]) u = Fa[u][i], v = Fa[v][i];
    return Fa[u][0];
}

void GetSize(int Now, int Fa) {
    Size[Now] = 1, Max[Now] = 0;
    for (int p = Last[Now]; p; p = Next[p]) {
        int v = Go[p];
        if (v == Fa || Flag[v]) continue;
        GetSize(v, Now);
        Size[Now] += Size[v];
        Max[Now] = max(Max[Now], Size[v]);
    }
}

void GetRoot(int Now, int Fa) {
    Max[Now] = max(Max[Now], Size[All] - Size[Now]);
    if (Max[Now] < Min) Min = Max[Now], Root = Now;
    for (int p = Last[Now]; p; p = Next[p]) {
        int v = Go[p];
        if (v == Fa || Flag[v]) continue;
        GetRoot(v, Now);
    }
}

int GetDis(int u, int v) {
    return Dis[u] + Dis[v] - 2 * Dis[Lca(u, v)];
}

void Update(int u, int id, int v) {
    vector<int> :: iterator p;
    for (int i = 1; i <= Son[v][0]; i ++) 
        for (p = VSon[v][i].begin(); p < VSon[v][i].end(); p ++) 
            VSon[u][id].push_back(*p);
    VSon[u][id].push_back(v);
    sort(VSon[u][id].begin(), VSon[u][id].end(), cmp);
    LL Sum = 0;
    for (p = VSon[u][id].begin(); p < VSon[u][id].end(); p ++) {
        int t = *p;
        Sum += LL(GetDis(t, u));
        VAge[u][id].push_back(Age[t]), VSum[u][id].push_back(Sum);
    }
}

int Divide(int Now) {
    Min = N, Root = All = Now;
    GetSize(Now, 0), GetRoot(Now, 0);
    int Rt = Root;
    Flag[Rt] = 1;
    for (int p = Last[Rt]; p; p = Next[p]) {
        int v = Go[p];
        if (Flag[v]) continue;
        int son = Divide(v);
        Pre[son] = Rt;
        Son[Rt][++ Son[Rt][0]] = son;
        Update(Rt, Son[Rt][0], son);
    }
    return Rt;
}

void Solve(int Now, int Not) {
    for (int i = 1; i <= Son[Now][0]; i ++) {
        if (Son[Now][i] == Not || VSon[Now][i].empty()) continue;
        p = lower_bound(VAge[Now][i].begin(), VAge[Now][i].end(), L);
        int l = lower_bound(VAge[Now][i].begin(), VAge[Now][i].end(), L) - VAge[Now][i].begin();
        int r = upper_bound(VAge[Now][i].begin(), VAge[Now][i].end(), R) - VAge[Now][i].begin();
        r --;
        if (r < l) continue;
        Ans += LL(GetDis(Now, u)) * LL(r - l + 1) + VSum[Now][i][r];
        if (l) Ans -= VSum[Now][i][l - 1];
    }
    if (Age[Now] <= R && Age[Now] >= L) Ans += LL(GetDis(Now, u));
    if (Pre[Now]) Solve(Pre[Now], Now);
}

int main() {
    freopen("shop.in", "r", stdin), freopen("shop.out", "w", stdout);

    scanf("%d%d%d", &N, &Q, &A);
    for (int i = 1; i <= N; i ++) scanf("%d", &Age[i]), D[i] = i;
    for (int i = 1; i < N; i ++) {
        int u, v, c;
        scanf("%d%d%d", &u, &v, &c);
        Link(u, v, c), Link(v, u, c);
    }
    GetDeep(1, 0, 0), GetFa();
    Divide(1);

    for (int i = 1; i <= Q; i ++) {
        int l, r;
        scanf("%d%d%d", &u, &l, &r);
        l = (l + Ans) % A, r = (r + Ans) % A;
        L = min(l, r), R = max(l, r), Ans = 0;
        Solve(u, 0);
        printf("%lld\n", Ans);
    }
}