poj1755 半平面交解不等式组

题目链接：http://poj.org/problem?id=1755

题意：铁人三项比赛，给出ｎ个人进行每一项的速度vi, ui, wi;  对每个人判断，通过改变3项比赛的路程，是否能让该人获胜（严格获胜）。

思路：题目实际上是给出了n个式子方程，Ti  = Ai * x + Bi * y + Ci * z ， 0 < i < n

          要判断第i个人能否获胜，即判断不等式组   Tj - Ti > 0,      0 < j < n && j != i    有解

        即 （Aj - Ai）* x + （Bj - Bi） * y + ( Cj - Ci ) * z > 0,   0 < j < n && j != i 有解

         由于 z > 0, 所以 可以两边同时除以 z， 将 x / z, y / z 分别看成 x和 y ， 这样就化三维为二维，可用半平面交判断是否存在解了，

         对每个人构造一次，求一次半平面交即可。

我用的ZZY的 I＆Ｓ算法的模版，做的过程中要将Ａ＊x + B * y + C > 0表示的半平面，转化成由两点组成的向量表示， IQ问题，纠结挺久

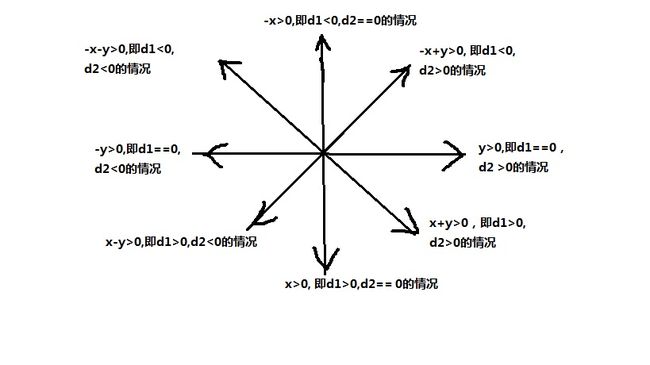
首先，所有的半平面保证符号一致（我取的> ), 然后根据 A， B， C的正负构造向量，下面随便画了个小图，帮助理解

我取的每个向量的左边为半平面， 图中 d1， d2就是代码中的，表示的A， B的正负

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

const double eps = 1e-10;
const double maxl = 1e10;
const int maxn = 105;

int dq[maxn], top, bot, pn, order[maxn], n, A[maxn], B[maxn], C[maxn];
struct Point {
    double x, y;
} p[maxn];

struct Line {
    Point a, b;
    double angle;
} tmpL[maxn];

int dblcmp(double k) {
    if (fabs(k) < eps) return 0;
    return k > 0 ? 1 : -1;
}

double multi(Point p0, Point p1, Point p2) {
    return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);
}

bool cmp(int u, int v) {
    int d = dblcmp(tmpL[u].angle-tmpL[v].angle);
    if (!d) return dblcmp(multi(tmpL[u].a, tmpL[v].a, tmpL[v].b)) > 0;
    return d < 0;
}

void getIntersect(Line l1, Line l2, Point& p) {
    double dot1,dot2;
    dot1 = multi(l2.a, l1.b, l1.a);
    dot2 = multi(l1.b, l2.b, l1.a);
    p.x = (l2.a.x * dot2 + l2.b.x * dot1) / (dot2 + dot1);
    p.y = (l2.a.y * dot2 + l2.b.y * dot1) / (dot2 + dot1);
}


bool judge(Line l0, Line l1, Line l2) {
    Point p;
    getIntersect(l1, l2, p);
    return dblcmp(multi(p, l0.a, l0.b)) <= 0;  /*此处有=，也就是交点p在 l0 上时， dq中最上面的半平面也去掉，因为题目要求严格获胜，也就是最终求出的
                                                                        半平面交为一个点，也认为是无法获胜的
                                                                     */
 }

void addLine(double x1, double y1, double x2, double y2, Line& l) {
    l.a.x = x1; l.a.y = y1;
    l.b.x = x2; l.b.y = y2;
    l.angle = atan2(y2-y1, x2-x1);
}

bool halfPlaneIntersection(Line l[], int n) {
    int i, j;

    for (i = 0; i < n; i++) order[i] = i;
    sort(order, order+n, cmp);
    for (i = 1, j = 0; i < n; i++)
        if (dblcmp(l[order[i]].angle-l[order[j]].angle) > 0)
            order[++j] = order[i];
    n = j + 1;
    dq[0] = order[0];
    dq[1] = order[1];
    bot = 0;
    top = 1;
    for (i = 2; i < n; i++) {
        while (bot < top && judge(l[order[i]], l[dq[top-1]], l[dq[top]])) top--;
        while (bot < top && judge(l[order[i]], l[dq[bot+1]], l[dq[bot]])) bot++;
        dq[++top] = order[i];
    }
    while (bot < top && judge(l[dq[bot]], l[dq[top-1]], l[dq[top]])) top--;
    while (bot < top && judge(l[dq[top]], l[dq[bot+1]], l[dq[bot]])) bot++;
    if (bot + 1 >= top) return false; //当dq中少于等于两条边时，说明半平面无交集
    return true;
}

void solve() {
    int i, j, k;
    double x1, y1, x2, y2, a, b, c;
   
   //给半平面加一个框，这样可以使解x，y都大于0，也可以避免所有半平面交起来后为不为凸多边形，而是一个敞开的区域
  //如果题目输入的不是一个多边形，而是本题这种输入若干不等式组的情况，这样的限定就是必须的，不然有bug，例如，两条线是平行的(但是极角不同)，
  //极角排序后又挨在一起, 那么就可能求它们的交点，就容易出错
   addLine(0, 0, maxl, 0, tmpL[0]);
    addLine(maxl, 0, maxl, maxl, tmpL[1]);
    addLine(maxl, maxl, 0, maxl, tmpL[2]);
    addLine(0, maxl, 0, 0, tmpL[3]);
    for (i = 0; i < n; i++) {
         bool flag = false;
         for (k = 4, j = 0; j < n; j++)
            if (i != j) {
                a = 1.0 / A[j] - 1.0 / A[i];
                b = 1.0 / B[j] - 1.0 / B[i];
                c = 1.0 / C[j] - 1.0 / C[i];
                int d1 = dblcmp(a);
                int d2 = dblcmp(b);
                int d3 = dblcmp(c);
                /*本人IQ较低，以下这段纠结一个小时。。。
                  下面是根据a*x+b*y+c>0取向量p1p2，
                  其中p1（x1，y1），p2（x2，y2）
                  就是将直线转化为以两点的表示，取向量p1p2左半为半平面
                */
                if (!d1) {
                    if (!d2) {
                        if (d3 <= 0) {
                            flag = true; break;
                        }
                        continue;
                    }
                    x1 = 0;
                    x2 = d2;//d2的值为1或-1
                    y1 = y2 = - c / b;
                }
                else {
                    if (!d2) {
                        x1 = x2 = - c / a;
                        y1 = 0;
                        y2 = -d1;
                    }
                    else {
                        x1 = 0; y1 = - c / b;
                        x2 = d2;
                        y2 = -(c + a * x2) / b;
                    }
                }
                addLine(x1, y1, x2, y2, tmpL[k]);
                k++;
            }
         if (flag || !halfPlaneIntersection(tmpL, k)) printf ("No\n");
         else printf ("Yes\n");
    }
}
int main()
{
    scanf ("%d", &n);
    for (int i = 0; i < n; i++)
        scanf ("%d%d%d", &A[i], &B[i], &C[i]);
    solve();

    return 0;
}