【POJ 3608】Bridge Across Islands
| Time Limit: 1000MS | Memory Limit: 65536K | |||
| Total Submissions: 8853 | Accepted: 2603 | Special Judge | ||
Description
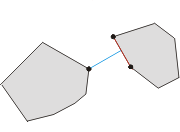
Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.
Input
The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].
Output
For each test case output the minimal distance. An error within 0.001 is acceptable.
Sample Input
4 4 0.00000 0.00000 0.00000 1.00000 1.00000 1.00000 1.00000 0.00000 2.00000 0.00000 2.00000 1.00000 3.00000 1.00000 3.00000 0.00000 0 0
Sample Output
1.00000
Source
求两个凸包的最近距离,旋转卡壳。
先把点变成逆时针顺序。
旋转卡壳用在两个凸包和用在一个凸包上的道理基本一致,但由于是最近距离,计算的时候分两种情况:
1.点到直线的距离
2.直线到直线的距离(平行的时候)
在求点到直线的距离的时候要注意如果点到直线的垂线的垂足不在线段上,那么最近距离就是点到线段两端点的距离。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cmath>
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
struct Point
{
double x,y;
}a[10005],b[10005];
int n,m;
double Cross(Point a,Point b,Point c)
{
return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
void anticlockwise(Point a[],int n)
{
for (int i=0;i<n-2;i++)
{
double tmp=Cross(a[i],a[i+1],a[i+2]);
if (tmp>eps) return;
else if (tmp<-eps)
{
reverse(a,a+n);
return;
}
}
}
double dis(Point a,Point b)
{
return sqrt((b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y));
}
double mult(Point a,Point b,Point c)
{
return (b.x-a.x)*(c.x-a.x)+(b.y-a.y)*(c.y-a.y);
}
double Getdis(Point a,Point b,Point c)
{
if (dis(a,b)<eps) return dis(b,c);
if (mult(a,b,c)<-eps) return dis(a,c);
if (mult(b,a,c)<-eps) return dis(b,c);
return fabs(Cross(a,b,c)/dis(a,b));
}
double mindis(Point a,Point b,Point c,Point d)
{
return min(min(Getdis(a,b,c),Getdis(a,b,d)),min(Getdis(c,d,a),Getdis(c,d,b)));
}
double Solve(Point a[],Point b[],int n,int m)
{
int ymina=0,ymaxb=0;
for (int i=0;i<n;i++)
if (a[i].y<a[ymina].y)
ymina=i;
for (int i=0;i<m;i++)
if (b[i].y<b[ymaxb].y)
ymaxb=i;
a[n]=a[0],b[m]=b[0];
double tmp,ans=inf;
for (int i=0;i<n;i++)
{
while (tmp=Cross(a[ymina+1],b[ymaxb+1],a[ymina])-Cross(a[ymina+1],b[ymaxb],a[ymina])>eps)
ymaxb=(ymaxb+1)%m;
if (tmp<-eps) ans=min(ans,Getdis(a[ymina],a[ymina+1],b[ymaxb]));
else ans=min(ans,mindis(a[ymina],a[ymina+1],b[ymaxb],b[ymaxb+1]));
ymina=(ymina+1)%n;
}
return ans;
}
int main()
{
while (scanf("%d%d",&n,&m)!=EOF)
{
if (!n&&!m) break;
for (int i=0;i<n;i++)
scanf("%lf%lf",&a[i].x,&a[i].y);
for (int i=0;i<m;i++)
scanf("%lf%lf",&b[i].x,&b[i].y);
anticlockwise(a,n);
anticlockwise(b,m);
printf("%.5lf\n",min(Solve(a,b,n,m),Solve(b,a,m,n)));
}
return 0;
}
感悟:
1.WA是因为求距离没有开根号
2.旋转卡壳对于两个凸包同样适用,只是一个凸包求直径时要求面积最大,两个凸包求最短距离要求面积最小